本文介绍我写的一个高颜值的、脱离了低级趣味的小程序：用 Python 和 POV-Ray 绘制各种三维多面体和四维多胞体，代码在 Github 上。

以下是用这个程序渲染的一些例子，其中不同颜色的顶点/边/面表示它们在对称群的作用下位于不同的轨道中，具体解释见后。

例子

• 所有的 Platonic 多面体，Archimedean 多面体，比如 snub dodecahedron:

• 所有的 Kepler-Poinsot 多面体，比如 great icosahedron:

• 所有的四维均匀多胞体 （除去一个特例 The grand antiprism），比如我的 Github 头像 (runcinated 120-cell)：

  

• 截断的四维正方体 truncated tesseract:

• 4d cube:

  

• 也可以是非凸的，比如星状正多胞体中的 grand stellated 120-cell:

• 甚至是 5 维欧氏空间中的均匀多胞体，如 5-cube:

等等，可玩的效果是非常多的。

以上这些都是在 Python 中做好计算以后，将多胞体的数据导出到 POV-Ray 中渲染得到的。你完全可以通过改写代码中的 POV-Ray 的部分来渲染得出不同的效果，当然前提是需要掌握 POV-Ray 的场景描述语言，不过这属于另一段故事，就不在本文的讨论范围内了。

下面介绍程序背后的数学原理。

这些图画的都是什么？

这些图都是三维或者四维欧氏空间中凸/非凸的均匀多胞体 (polytope)，三维的情形更常用的称呼是多面体。这里有几个关键词需要注意：凸/非凸、均匀。

凸比较好理解，就是指多胞体上任意两点间的连线仍然属于此多胞体，否则就是非凸。上面的例子中 Platonic 多面体、Archimedean 多面体都是凸的，Kepler-Poinsot 多面体、星状正多胞体都是非凸的。

均匀这个词就不太好理解了。简单说就是：多胞体的所有顶点都一样，且每个面都是正多边形，每个胞腔都是三维的均匀多面体（这是个递归的定义）。

要准确解释什么叫所有顶点都一样，就要用到群论的语言：一个多胞体 \(P\) 的对称群 \(G\) 是欧氏空间中一组正交变换构成的有限群，\(G\) 作用在 \(P\) 上保持 \(P\) 不变。所有顶点都一样的严格说法是 \(G\) 传递地作用在 \(P\) 的顶点集上，即对 \(P\) 的任何两个顶点 \(u,v\)，都存在 \(g\in G\)，\(g\) 把 \(u\) 映射为 \(v\)。

这些图是怎么画出来的？

这些多胞体看起来样子大不相同，但它们都可以用同一种方法计算出来，叫做 Wythoff 构造法，也称万花筒构造法。它的原理跟我们小时候玩的万花筒的原理是一样的：在空间中放置若干过原点的反射平面 （镜子），镜面之间的夹角是精心设计好的，都形如 \(\pi-\pi/p\)，其中 \(p\) 为有理数。在空间中选定一个初始顶点 \(v_0\)，将 \(v_0\) 关于这些镜子反复作反射变换，得到的全部镜像就是多胞体的顶点。如果 \(v_0\) 关于第 \(i\) 面镜子反射后得到的镜像是 \(v_1\)，则 \((v_0,v_1)\) 构成一条类型为 \(i\) 的边，我们把它以及在对称群作用下同轨道的所有边都染成 \(i\) 号色。如果 \(v_0\) 先关于镜面 \(i\) 作反射，再关于镜面 \(j\) 作反射，则由于两个反射变换的复合是一个旋转变换，\(v_0\) 实际上是绕着某个面的中心和原点的连线作了一次旋转，旋转的角度为 \(2\pi/m\) （假设镜面 \(i\) 和镜面 \(j\) 的法向量夹角是 \(\pi-\pi/m\)），重复此旋转 \(m\) 次即可得到多胞体的一个类型为 \((i,j)\) 的面，我们把它在对称群作用下同轨道的所有面都染成同一颜色。

这里的关键问题有两个：

1. 对于不同的均匀多胞体，应该如何放置这些镜面，并选择初始顶点？
2. 摆好镜面和初始顶点以后，怎样不重复不遗漏地计算初始顶点的所有镜像？

第一个问题的答案叫做 Coxeter-Dynkin 图，Coxeter-Dynkin 图是一个带标记信息的无向图，它编码了多胞体的全部信息，即只要知道了多胞体对应的 Coxeter-Dynkin 图，就可以求出该多胞体的所有数据 （仅缩放大小和在空间中的摆放位置除外）。每个均匀多胞体都有一个 Coxeter-Dynkin 图与之对应，但是不同的 Coxeter-Dynkin 图可能描述的是相同的多胞体。

比如正方体的 Coxeter-Dynkin 图为：

我们来解释这个图的含义：

在一个 Coxeter-Dynkin 图中，每个顶点代表一面镜子，在上图中有三个顶点，所以有三面镜子。将这三面镜子从左到右依次记作 \(m_0, m_1, m_2\)，顶点之间的边记录了镜子间的夹角：

1. 若两个镜面之间的夹角为 \(\pi/2\) 则它们之间没有边相连。
2. 若两个镜面之间的夹角为 \(\pi-\pi/3\) 则它们之间用一条无标记的边相连。
3. 若两个镜面之间的夹角为 \(\pi-\pi/m\) (\(m\) 为有理数且 \(m>2, m\ne3\))，则它们之间用一条标号为 \(m\) 的边相连。

此外用圈出的镜面来标记初始顶点的位置，一个镜面被圈出当且仅当初始顶点不在这个镜面上。

从而在正方形的情形 \(\langle m_0,m_1\rangle=\pi-\pi/4\)，\(\langle m_1,m_2\rangle=\pi-\pi/3\)，\(\langle m_0,m_2\rangle=\pi/2\)。初始顶点落在 \(m_1\) 和 \(m_2\) 上但是不属于 \(m_0\)。

于是这三面镜子可以这样摆放：

1. 镜子 \(m_0\) 的法向量可以随意，比如 \(n_0=(1, 0, 0)\)。
2. 镜子 \(m_1\) 的法向量 \(n_1\) 与 \(n_0\) 夹角为 \(3\pi/4\)，于是 \(n_1\) 可以取为 \((\cos\dfrac{3\pi}{4}, \sin\dfrac{3\pi}{4}, 0)\)。
3. 镜子 \(m_2\) 的法向量 \(n_2\) 与 \(n_0\) 垂直，所以 \(n_2\) 形如 \((0,y_3,z_3)\)，它与 \(n_1\) 夹角是 \(2\pi/3\)，所以 \(y_3 \sin\dfrac{3\pi}{4}=\cos\dfrac{2\pi}{3}\)，再结合 \(n_2\) 是单位向量，\(z_3=\sqrt{1-y_3^2}\)，解出 \(y_3, z_3\) 即可。

要选择一个落在 \(m_1\) 和 \(m_2\) 上但是不落在 \(m_0\) 上的初始点 \(v_0\)，我们可以让 \(v_0\) 到平面 \(m_1\) 和 \(m_2\) 的距离为 0，到平面 \(m_0\) 的距离为 1，即

\[\langle v_0, n_0\rangle=1,\quad \langle v_0, n_1\rangle=0,\quad\langle v_0, n_2\rangle=0.\]

求解这个线性方程组即可。

我们前面提到过，要使得初始顶点的所有镜像恰好构成一个均匀多胞体，镜子之间的夹角必须精心设置，这实际上只有有限种可能。换句话说，只有有限个 Coxeter-Dynkin 图可以给出 3D/4D 的均匀多胞体。在 维基百科 上完整的列出了每种均匀多胞体对应的 Coxeter-Dynkin 图，这里就不再专门列举了，但是特别指出两点：

1. Coxeter-Dynkin 图的标号完全决定了多胞体的对称性，而初始顶点的位置则决定了多胞体的截断类型。
2. 对偶的多胞体具有相同的 Coxeter-Dynkin 图，只不过要把边的标号从右到左反过来。比如正八面体和正方体的 Coxeter-Dynkin 图是一样的，但是边的标号是 (3, 4)。

第二个问题的答案叫做 Todd-Coxeter 算法，展开讲的话比较复杂，我们单列一节专门谈谈。

有限表现群和 Todd-Coxeter 算法

怎样求出初始顶点在所有镜子中的镜像？有个简单的办法：只要反复地将初始顶点关于每个镜面作反射，算出得到的镜像点的坐标，并与之前得到的点的坐标相比较（浮点数比较需要在一定的误差范围内考虑），直到不再有新的镜像点出现为止，不就得到全部顶点集吗？这个方法确实可行，但是既笨又丑陋：它完全没有用到多胞体具有对称性这一事实！

这个程序采用的是基于符号计算的途径，这个方法可以精准地得出所有顶点/边/面的信息，代价就是涉及的数学略复杂。我们先回忆一下群在集合上的作用的轨道—稳定化子定理：

这个定理告诉我们，如果群 \(G\) 传递地作用在一个集合 \(S\) 上，而且对 \(S\) 中某个元素 \(x\) 我们知道了它的稳定化子群 \(H\)，则只要对 \(G/H\) 的每个陪集代表元 \(g\)，将 \(g\) 作用在 \(x\) 上就可以得到整个 \(S\)。

于是给定一个均匀多胞体 \(P\)，要求出其全部顶点集合，我们只要：

1. 根据 \(P\) 的 Coxeter-Dynkin 图确定其对称群 \(G\) 和初始顶点 \(v_0\)。
2. 定出 \(v_0\) 的稳定化子群 \(H\) 并求出 \(G/H\) 的一组陪集代表元。
3. 将 \(G/H\) 中的每个陪集代表元作用在 \(v_0\) 上即得 \(P\) 的全部顶点。

我们仍然以正方体为例来讲解：正方体的 Coxeter-Dynkin 图是

仍然记三个镜面为 \(m_0,m_1,m_2\)，其法向量分别为 \(n_0,n_1,n_2\)，设 \(\rho_0,\rho_1,\rho_2\) 分别是关于它们的反射变换，\(\rho_i\) 对应的矩阵为 \(M_i=I-2n_in_i^T\)（见 Householder 变换）。

正方体的对称群 \(G\) 由 \(\rho_0,\rho_1,\rho_2\) 这三个基本反射生成，其表现为： \[G = \langle\rho_0,\rho_1,\rho_2\ |\ \rho_0^2=\rho_1^2=\rho_2^2=(\rho_0\rho_1)^4=(\rho_1\rho_2)^3=(\rho_0\rho_2)^2=1\rangle.\] 这是因为反射的平方总是恒等变换，所以 \(\rho_i^2=1\)。\(\rho_0,\rho_1\) 是两个夹角为 \(3\pi/4\) 的反射，所以 \(\rho_0\rho_1\) 是一个角度为 \(3\pi/2\) 的旋转，旋转轴为 \(m_0\) 和 \(m_1\) 的交线，从而 \((\rho_0\rho_1)^4=1\)。\(\rho_1\rho_2,\rho_0\rho_2\) 的情形是类似的。¹

利用 Todd-Coxeter 算法 （后面有解释） 不难求出这个群包含 48 个元素，罗列如下： \[\begin{array}{lll}e&\rho_{0}&\rho_{0}\rho_{1}\\ \rho_{0}\rho_{1}\rho_{0}&\rho_{0}\rho_{1}\rho_{0}\rho_{1}&\rho_{1}\rho_{0}\rho_{1}\\\rho_{1}\rho_{0}&\rho_{1}&\rho_{0}\rho_{2}\\\rho_{2}&\rho_{1}\rho_{2}&\rho_{1}\rho_{2}\rho_{1}\\\rho_{2}\rho_{1}&\rho_{0}\rho_{1}\rho_{2}&\rho_{0}\rho_{1}\rho_{2}\rho_{1}\\\rho_{0}\rho_{2}\rho_{1}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}&\rho_{0}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\\\rho_{0}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}&\rho_{1}\rho_{0}\rho_{1}\rho_{2}\\\rho_{1}\rho_{0}\rho_{2}&\rho_{1}\rho_{0}\rho_{2}\rho_{1}&\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}\\\rho_{2}\rho_{1}\rho_{0}&\rho_{2}\rho_{1}\rho_{0}\rho_{1}&\rho_{0}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\\\rho_{0}\rho_{2}\rho_{1}\rho_{0}&\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}&\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\\\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}&\rho_{1}\rho_{2}\rho_{1}\rho_{0}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}\\\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}\rho_{1}&\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}&\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}\\\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}&\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}&\rho_{0}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\\\rho_{0}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}&\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}&\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\\\rho_{0}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}&\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}&\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\\\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}&\rho_{0}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\rho_{1}\rho_{0}\rho_{1}\rho_{2}\end{array} \] 由于在正方形的 Coxeter-Dynkin 图中只有镜面 \(m_0\) 是被圈出的，即初始顶点 \(v_0\) 落在 \(m_1\) 和 \(m_2\) 上，但不属于 \(m_0\)，所以反射 \(\rho_1,\rho_2\) 保持 \(v_0\) 不动，\(\rho_0\) 将 \(v_0\) 映射为其关于 \(m_0\) 的镜像，于是 \(v_0\) 的稳定化子群是 ² \[H=\langle \rho_1, \rho_2\ |\ \rho_1^2=\rho_2^2=(\rho_1\rho_2)^3=e\rangle.\] 显然 \(H\) 就是二面体群 \(D_3\)，所以 \(|H|=6\)，从而 \(|G/H|=8\)。利用 Todd-Coxeter 算法可得其一组右陪集代表元为 \[\begin{array}{llll}e&\rho_{0}&\rho_{0}\rho_{1}&\rho_{0}\rho_{1}\rho_{0}\\\rho_{0}\rho_{1}\rho_{2}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}\end{array} \] 将它们作用在 \(v_0\) 上即可得到正方体的 8 个顶点。例如 \(\rho_0\rho_1\) 作用在 \(v_0\) 上为 \[v_0(\rho_0\rho_1)=(v_0\rho_0)\rho_1=(v_0M_0)\rho_1=v_0M_0M_1.\] 其中 \(v_0\) 写成行向量的形式，每个 \(M_i\) 是对称矩阵。

计算边/面/胞腔的原理是类似的，但考虑的细节要多一些。比如我们想求出所有关于第 \(i\,(i=0,1,2)\) 个镜面 \(m_i\) 反射生成的类型为 \(i\) 的边，可以这样做：

1. 检查初始顶点 \(v_0\) 是否落在 \(m_i\) 上。如果答案为是，那么关于此镜面的反射保持 \(v_0\) 不变，此多面体不含类型 \(i\) 的边。否则设 \(v_0\) 关于 \(m_i\) 的镜像为 \(v_1\)，则 \((v_0, v_1)\) 构成一条类型为 \(i\) 的边 \(e\)。
2. 关于 \(m_i\) 的反射 \(\rho_i\) 把 \(v_0\) 和 \(v_1\) 互换，从而保持 \(e\) 不变。注意其它任何与 \(m_i\) 垂直并且包含初始点 \(v_0\) 的镜面反射也会保持 \(e\) 不变。在正方形的情形中，反射 \(\rho_0\) 互换 \(e\) 的两端因而保持 \(e\) 不变，此外镜面 \(m_0\) 和 \(m_2\) 是垂直的，且 \(v_0\) 包含在 \(m_2\) 中，所以反射 \(\rho_2\) 保持 \(e\) 上的每个点不变，于是 \(e\) 的稳定化子群为 \(H=\langle \rho_0,\rho_2 \rangle\)。显然 \(H\) 同构于 \(\mathbb{Z}_2\times\mathbb{Z}_2\)，所以 \(|H|=4\)，从而 \(|G/H|=12\)，即正方体有 12 条边 ³。
3. 求出 \(G/H\) 的一组陪集代表元并作用在 \(e\) 上得出全部类型为 \(i\) 的边。

求面的情形复杂一些，基本原理是这样的：

1. 对 \(i\ne j\)，如果初始顶点 \(v_0\) 不同时属于镜面 \(i\) 和镜面 \(j\)，则旋转 \(\rho_i\rho_j\) 就可以生成一个面 \(f\)。需要注意的是，如果这两个镜面恰好垂直，则必须二者均不包含 \(v_0\) 才能得到一个非退化的面，这个面是个正方形。在正方体的情形，\(\rho_0\rho_1\) 可以生成一个面，\(\rho_0\rho_2\)（两镜面垂直但只有一个镜面包含 \(v_0\)）和 \(\rho_1\rho_2\)（两镜面均包含 \(v_0\)）都不能给出面。
2. \(f\) 的稳定化子群是由 \(\rho_i,\rho_j\) 和那些包含 \(v_0\) 且与 \(m_i,m_j\) 均垂直的镜面反射生成。在正方形的情形是 \(H=\langle \rho_0,\rho_1 \rangle\) ⁴，显然 \(H\) 同构于二面体群 \(D_8\)，因此 \(|H|=8\)，\(|G/H|=6\)，即正方体有 6 个面。

总之关键的步骤都是给定群 \(G\) 和某个子群 \(H\)，求 \(G/H\) 的一组陪集代表元。

这里用到的算法叫做 Todd-Coxeter 算法。

Todd-Coxeter 算法在许多抽象代数或者群论的教材都有，用到的数学知识并不复杂。但完整描述并证明一份程序实现的细节还是很费功夫的，恐怕要好几页纸才能说清楚。限于篇幅，我这里仅用正方体的情形为例说明算法的步骤，具体的证明和更多的细节读者请参考

Handbook of Computational Group Theory, Holt, D., Eick, B., O’Brien, E.

中的 coset enumeration 一章。我个人认为这是讲解 Todd-Coxeter 算法最棒的文献。

Todd-Coxeter 算法非常类似玩数独游戏，这里要填的表是一个变化的二维数组 \(T\)，\(T\) 的行 \(i\) 代表第 \(i\) 个右陪集，\(T\) 的列 \(j\) 代表第 \(j\) 个生成元 \(\rho_j\)，\(T[i][j]\) 的值等于 \(\rho_j\) 右乘以第 \(i\) 个陪集后得到的陪集。初始时，我们知道肯定有一个陪集，就是 \(H\) 自身，还有没有其它的陪集我们不清楚。算法的主要流程就是根据 \(G\) 和 \(H\) 的表现中包含的关系来发现新的陪集并填入表中，直到无法找到新的陪集为止。最终得到的 \(T\) 实际上是 \(G/H\) 的 schreier 图的邻接矩阵，它记录了 \(G/H\) 的陪集间的乘法关系，由 \(T\) 出发我们很容易求出这些陪集的 word 表示。

我们先罗列一下这个数独游戏已知的关系：

已知关系：

1. 对 \(H\) 的任何生成字 \(w\) 有 \(H\cdot w=H\)，即 \(H\rho_1=H\rho_2=H\)。注意此关系仅要求对 \(H\) 成立。
2. 对任何陪集 \(K\) 和 \(G\) 的任何生成关系 \(r\) 有 \(K\cdot r=K\)，即 \(K\rho_i^2=K, i=0,1,2\) 以及 \(K(\rho_0\rho_1)^4=K(\rho_1\rho_2)^3=K(\rho_0\rho_2)^2=K\)。注意此关系要求对所有陪集成立。

这些关系可以存储在两个列表里面，每个关系用一个数组表示。

第一个列表存储的是 \(H\) 的生成字，即

\(H\) 的生成字列表：

0. (1,)
1. (2,)

第二个列表存储的是 \(G\) 的生成关系，即

\(G\) 的生成关系列表：

2. (0, 0)
3. (1, 1)
4. (2, 2)
5. (0, 1, 0, 1, 0, 1, 0, 1)
6. (1, 2, 1, 2, 1, 2)
7. (0, 2, 0, 2)

其中每条关系前面的数字是我们加上的编号以便于称呼。

初始时刻表格 \(T\) 是这样的：

	\(\rho_0\)	\(\rho_1\)	\(\rho_2\)
\(H_0\)	\(\phantom{}\)	\(\phantom{}\)	\(\phantom{}\)

其中 \(H_0\) 代表 \(H\) 对应的陪集。程序首先验证 \(H_0\) 所在的行满足第一个关系列表 （\(H\) 的生成字列表，随后此列表可以被丢弃），然后依次从上到下扫描 \(T\) 的每一行，假设当前扫描的是第 \(i\) 行，对应的陪集为 \(H_i\)，程序验证确保对第二个列表 （\(G\) 的生成关系列表） 中的每条关系 \(w\)，\(H_i\) 满足 \(H_iw=H_i\)，这个过程中可能发现新的陪集，也可能发现已有的某些陪集是重复的，也有可能需要强行定义新的陪集来使得这个验证能够完成。

---

我们来开始扫描 \(H_0\) 所在的行：首先检查第一个列表中的关系，这个列表仅在扫描 \(H_0\) 时使用一次，扫描完就可以丢弃。

(1). 对第 0 条关系 \(H_0\rho_1=H_0\)，即 \(T[0][1]=0\)。对第 1 条关系 \(H_0\rho_2=H_0\)，即 \(T[0][2]=0\)，这时 \(T\) 变成了

	\(\rho_0\)	\(\rho_1\)	\(\rho_2\)
\(H_0\)	\(\phantom{}\)	0	0

第一个列表扫描完毕，接下来扫描第二个列表。

(2). 对第 2 条关系 \(H_0\rho_0^2=H_0\)，由于 \(H_0\rho_0\) 还不知道，我们将其定义为新陪集 \(H_1\) 并将 1 填入 \(T[0][0]\) 位置，此外还要为 \(H_1\) 开辟新的一行：

	\(\rho_0\)	\(\rho_1\)	\(\rho_2\)
\(H_0\)	1	0	0
\(H_1\)	0	\(\phantom{}\)	\(\phantom{}\)

(3). 第 3 条和第 4 条关系已经满足，继续。

(4). 第 5 条关系，\(H_0\rho_0\rho_1\rho_0\rho_1\rho_0\rho_1\rho_0\rho_1=H_0\)，我们已经知道 \(H_0\rho_0=H_1\) 但是 \(H_1\rho_1\) 还不知道，将其定义为 \(H_2\)，于是 \(T\) 中又添两项，并开辟新的一行给 \(H_2\)：

\(\phantom{}\)	\(\rho_0\)	\(\rho_1\)	\(\rho_2\)
\(H_0\)	1	0	0
\(H_1\)	0	2	\(\phantom{}\)
\(H_2\)	\(\phantom{}\)	1	\(\phantom{}\)

但是 \(H_2\rho_0\) 还是不知道，所以继续定义 \(H_2\rho_0=H_3\)，于是 \(T\) 变成

	\(\rho_0\)	\(\rho_1\)	\(\rho_2\)
\(H_0\)	1	0	0
\(H_1\)	0	2	\(\phantom{}\)
\(H_2\)	3	1	\(\phantom{}\)
\(H_3\)	2	\(\phantom{}\)	\(\phantom{}\)

于是现在关系变成了

\[\underbrace{\overbrace{\underbrace{H_0\rho_0}_{=H_1}\,\rho_1}^{=H_2}\,\rho_0}_{=H_3}\,\rho_1\rho_0\rho_1\rho_0\rho_1=H_0.\]

但是 \(H_3\rho_1\) 还是不知道，你可能会想把它继续定义为新的陪集 \(H_4\)，然后继续扫描。这样做不是不可以，但是每次都定义新陪集会生成大量重复的陪集，导致 \(T\) 增长的非常快，对更复杂的群非常耗费计算资源。我们采用更聪明的办法：倒着扫描整个关系，即从右到左扫描 \(H_0\rho_0\rho_1\rho_0\rho_1\rho_0\rho_1\rho_0\rho_1=H_0\) 这条关系。记住我们现在已经正向 （从左到右） 扫描到了下面的位置： \[\underbrace{H_0\rho_0\rho_1\rho_0}_{=H_3}\,\rho_1|\rho_0\rho_1\rho_0\rho_1=H_0.\] 反向扫描意味着我们把上式左边末尾的 \(\rho_0\rho_1\rho_0\rho_1\) 挪到右边去，变形为 \[\underbrace{H_0\rho_0\rho_1\rho_0}_{=H_3}\,\rho_1=\underbrace{H_0\rho_1}_{=H_0}\rho_0\rho_1\rho_0=H_0\rho_0\rho_1\rho_0= H_3.\] 从而 \(H_3\rho_1=H_3\)。这样通过反向扫描我们就推断出了 \(H_3\rho_1\) 的值，避免了定义冗余的陪集。按照 Holt 书中的说法这叫做一个 deduction。这时 \(T\) 为

	\(\rho_0\)	\(\rho_1\)	\(\rho_2\)
\(H_0\)	1	0	0
\(H_1\)	0	2	\(\phantom{}\)
\(H_2\)	3	1	\(\phantom{}\)
\(H_3\)	2	3	\(\phantom{}\)

(5). 关系 6 已经满足，继续。

(6). 对关系 7 \(H_0\rho_0\rho_2\rho_0\rho_2=H_0\)，从两头扫描我们得到 \[\underbrace{H_0\rho_0}_{=H_1}\,\rho_2=\underbrace{\overbrace{H_0\rho_2}^{=H_0}\rho_0}_{=H_1}.\] 即 \(H_1\rho_2=H_1\)，我们又得到了一个 deduction，从而 \(T\) 变成

	\(\rho_0\)	\(\rho_1\)	\(\rho_2\)
\(H_0\)	1	0	0
\(H_1\)	0	2	1
\(H_2\)	3	1	\(\phantom{}\)
\(H_3\)	2	3	\(\phantom{}\)

至此对 \(H_0\) 的扫描全部完成，我们转入扫描 \(H_1\) 所在的行。

---

注意：从现在起至程序结束，我们不再使用第一个列表。

下面开始扫描 \(H_1\) 所在的行。

(1). 经检查关系 2, 3, 4, 5 已经满足，继续。

(2). 对关系 6 有 \(H_1\rho_1\rho_2\rho_1\rho_2\rho_1\rho_2=H_1\)，其中 \(H_1\rho_1=H_2\) 已知但 \(H_2\rho_2\) 未知。反向的扫描也会卡在这里： \[\underbrace{H_1\rho_1}_{=H_2}\rho_2\rho_1=H_1\rho_2\rho_1\rho_2=H_2\rho_2.\] 所以我们定义新陪集 \(H_2\rho_2=H_4\)，于是 \(H_4\rho_1=H_4\)，从而此时 \(T\) 为

	\(\rho_0\)	\(\rho_1\)	\(\rho_2\)
\(H_0\)	1	0	0
\(H_1\)	0	2	1
\(H_2\)	3	1	4
\(H_3\)	2	3	\(\phantom{}\)
\(H_4\)	\(\phantom{}\)	4	2

(3). 关系 7 已经满足，从而 \(H_1\) 检查完毕，接下来开始扫描 \(H_2\) 的行。

---

下面开始扫描 \(H_2\) 的行。

(1). 经检查关系 2, 3, 4, 5, 6 都已经满足，继续。

(2). 对关系 7 有 \(H_2\rho_0\rho_2\rho_0\rho_2=H_2\)，两边同时扫描的结果为： \[\underbrace{H_2\rho_0}_{=H_3}\rho_2\rho_0=H_2\rho_2=H_4.\] 即 \(H_3\rho_2\rho_0=H_4\)，但是继续正向扫描 \(H_3\rho_2\) 不知道，继续反向扫描 \(H_4\rho_0\) 不知道。定义新陪集 \(H_3\rho_2=H_5\)，于是 \(H_5\rho_0=H_4\)，我们又可以填入两对 4 个数字，此时 \(T\) 为：

	\(\rho_0\)	\(\rho_1\)	\(\rho_2\)
\(H_0\)	1	0	0
\(H_1\)	0	2	1
\(H_2\)	3	1	4
\(H_3\)	2	3	5
\(H_4\)	5	4	2
\(H_5\)	4	\(\phantom{}\)	3

\(H_2\) 扫描完毕，下面扫描 \(H_3\) 的行。

---

我把 \(H_3, H_4, H_5\) 的扫描过程留给你作为练习，\(H_3\) 扫描结束后你得到的 \(T\) 应该如下图：

	\(\rho_0\)	\(\rho_1\)	\(\rho_2\)
\(H_0\)	1	0	0
\(H_1\)	0	2	1
\(H_2\)	3	1	4
\(H_3\)	2	3	5
\(H_4\)	5	4	2
\(H_5\)	4	6	3
\(H_6\)	\(\phantom{}\)	5	6

\(H_4\) 扫描结束后你得到的 \(T\) 应该如下图：

	\(\rho_0\)	\(\rho_1\)	\(\rho_2\)
\(H_0\)	1	0	0
\(H_1\)	0	2	1
\(H_2\)	3	1	4
\(H_3\)	2	3	5
\(H_4\)	5	4	2
\(H_5\)	4	6	3
\(H_6\)	7	5	6
\(H_7\)	6	7	\(\phantom{}\)

\(H_5\) 的扫描给不出新的信息。

扫描 \(H_6\) 时，关系 2, 3, 4, 5, 6 都已经满足，由关系 7 \(H_6\rho_0\rho_2\rho_0\rho_2=H_6\) 可得 deduction \(H_7\rho_2=H_7\)，于是 \(T\) 可以补全为

	\(\rho_0\)	\(\rho_1\)	\(\rho_2\)
\(H_0\)	1	0	0
\(H_1\)	0	2	1
\(H_2\)	3	1	4
\(H_3\)	2	3	5
\(H_4\)	5	4	2
\(H_5\)	4	6	3
\(H_6\)	7	5	6
\(H_7\)	6	7	7

扫描 \(H_7\) 发现所有关系都已经满足。

至此 \(T\) 的空白位置都已经填满，没有新的陪集可以发现，数独游戏结束，这时得到的 \(T\) 就是 \(G/H\) 的最终乘法表。

由此利用宽度优先搜索不难得出陪集间的关系为： \[\begin{array}{l}H_0 = H_0\cdot e,\\ H_1=H_0\cdot\rho_0,\\H_2=H_1\cdot\rho_1=H_0\cdot\rho_0\rho_1,\\H_3=H_2\cdot\rho_0=H_0\cdot\rho_0\rho_1\rho_0,\\ H_4=H_2\cdot\rho_2=H_0\cdot\rho_0\rho_1\rho_2,\\ H_5=H_3\cdot\rho_2=H_0\cdot \rho_0\rho_1\rho_0\rho_2,\\ H_6=H_5\cdot\rho_1=H_0\cdot \rho_0\rho_1\rho_0\rho_2\rho_1,\\ H_7=H_6\cdot\rho_0=H_0\cdot \rho_0\rho_1\rho_0\rho_2\rho_1\rho_0.\end{array}\]

从而其一组陪集代表元可以选为 \[\begin{array}{llll}e&\rho_{0}&\rho_{0}\rho_{1}&\rho_{0}\rho_{1}\rho_{0}\\\rho_{0}\rho_{1}\rho_{2}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}&\rho_{0}\rho_{1}\rho_{0}\rho_{2}\rho_{1}\rho_{0}\end{array}\]

这正是我们前面看到过的。

星状多胞体的计算

星状多胞体也可以使用 Wythoff 构造法来生成，但是直接套用上面的方法一般是行不通的，我们需要在生成元中加入额外的生成关系。

这里以 Great dodecahedron 为例来说明：其 Coxeter-Dynkin 图为

于是三面镜子的法向量夹角分别为 \(\pi-2\pi/5, \pi/2, \pi-\pi/5\)。如果我们仍然沿用以前的分析，会得出其对称群的表现为 \[K=\langle\tau_0,\tau_1,\tau_2 \ |\ \tau_0^2=\tau_1^2=\tau_2^2=(\tau_0\tau_1)^5=(\tau_1\tau_2)^5=(\tau_0\tau_2)^2=1\rangle.\]

这是一个无限群，而且顶点的稳定化子的商群也是无限的，所以还想按以前的方法计算就行不通了。

实际上我们只要在生成关系中再加上一条 \((\tau_0\tau_1\tau_2\tau_1)^3=1\) 即可，即对称群的表现为

\[\begin{align*} K = \langle\tau_0,\tau_1,\tau_2 \ |\ &\tau_0^2=\tau_1^2=\tau_2^2=(\tau_0\tau_1)^5=(\tau_1\tau_2)^5=\\&(\tau_0\tau_2)^2=(\tau_0\tau_1\tau_2\tau_1)^3=1\rangle. \end{align*}\]

注意到我使用了字母 \(\tau\) 来表示反射，\(K\) 表示 Great dodecahedron 的对称群，这个记号选择是有意的。这是怎么回事呢？先看视频：

（请忽略左边错误的 Coxeter 图，这个 ui 界面我改不动）

由视频可见，Great dodecahedron 与正二十面体 (icosahedron) 共用相同的顶点，并且看起来 Great dodecahedron 可以通过在 icosahedron 表面挖一些三角形的洞得到。这个结论也可以推广：一般地如果星状多面体的洞是一个有 \(h\) 条边的多边形，则对应的额外生成关系就是 \((\tau_0\tau_1\tau_2\tau_1)^h=1\)。

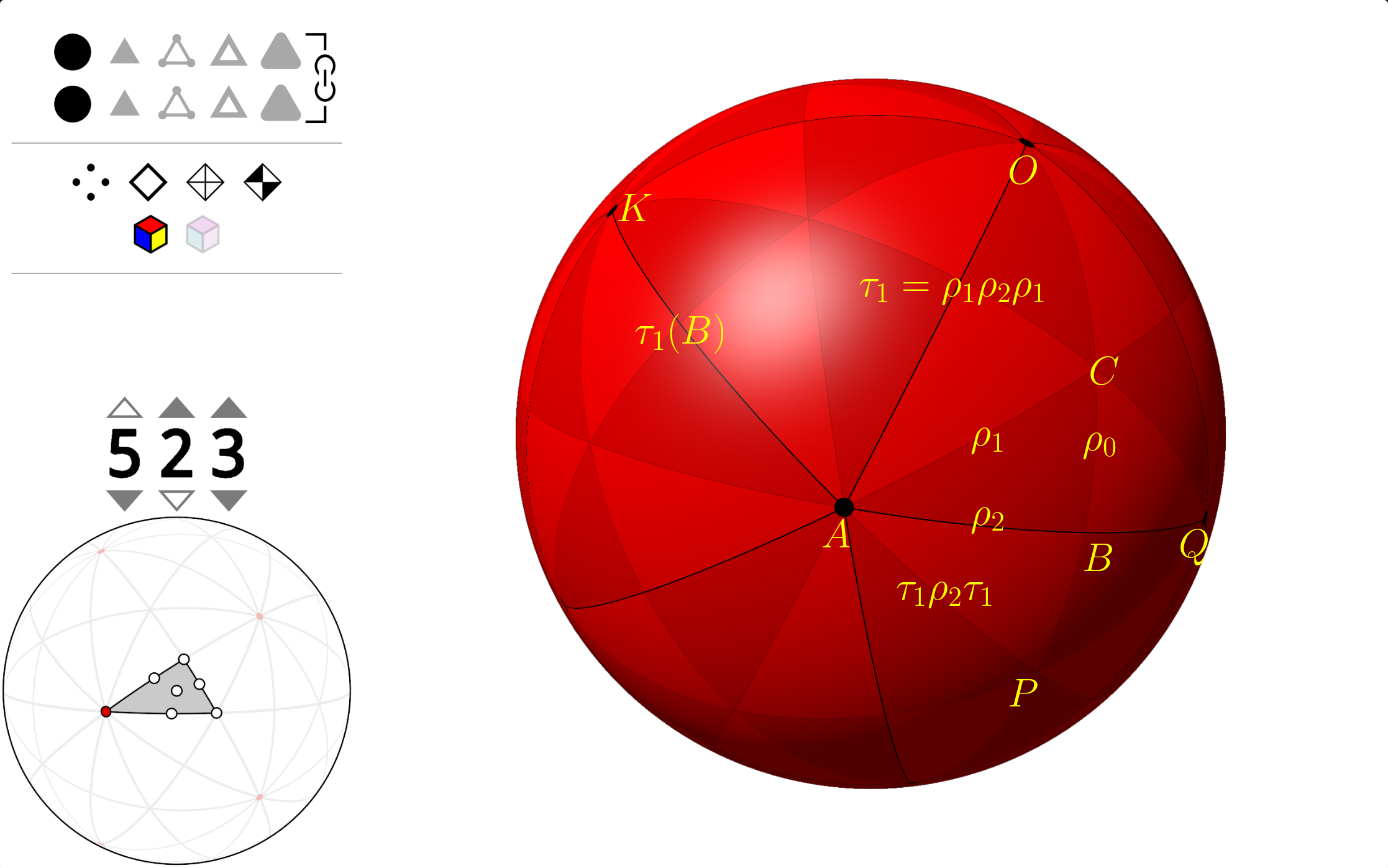
在上图中，\(\Delta ABC\) 是正二十面体的基本区域，三个内角分别是 \(\angle CAB=\pi/5\)，\(\angle CBA=\pi/2\)，\(\angle ACB=\pi/3\)，\(\rho_0,\rho_1,\rho_2\) 分别是关于弧 \(BC, AC, AB\) 的反射。正二十面体的对称群的表现为 \[G = \langle\rho_0,\rho_1,\rho_2\ |\ \rho_0^2=\rho_1^2=\rho_2^2=(\rho_0\rho_1)^3=(\rho_1\rho_2)^5=(\rho_0\rho_2)^2=1\rangle.\]

Great dodecahedron 可以这样得到：沿着正二十面体的边从顶点 \(Q\) 走到 \(A\)，右手边的面是三角形 \(\Delta OAQ\)，接下来的第一条边应该是 \(AO\)，我们跳过这条边，选择第二条边 \(AK\)，到达 \(K\) 后继续选择右手边的第二条边，这样绕着 \(O\) 一圈下来共经过 5 条边，它们正好围成 Great dodecahedron 的一个面。对正二十面体的其它边也如此操作会得到 Great dodecahedron 其它的面。

像这样对一个多面体，保持它的顶点和边的集合不变，但是每次选择右手边的第 \(k\) 个边走下去绕一圈获得一个面，这样构造新多面体的方法叫做 Facetting 手术。在我们这个项目中 \(k\) 总是等于 2。

我们来导出正二十面体的对称群 \(G\) 和 Great dodecahedron 的对称群 \(K\) 之间的关系。

来看三角形 \(\Delta OAB\)，它的三个内角分别是 \(\angle OAB=2\pi/5\)，\(\angle OBA=\pi/2\)，\(\angle AOB=\pi/5\)，它包含三个与 \(\Delta ABC\) 全等的三角形，关于其三条边 \(OA,OB,AB\) 的反射分别是 \(\tau_1=\rho_1\rho_2\rho_1,\tau_0=\rho_0,\tau_2=\rho_2\) ⁵。

Facetting 操作 \(\varphi_k\) 用群的语言来描述就是（记住 \(k=2\)） \[G=\langle \rho_0,\rho_1,\rho_2\rangle\xrightarrow{\ \varphi_k\ }\langle\rho_0,\rho_1(\rho_2\rho_1)^{k-1},\rho_2\rangle=\langle\tau_0,\tau_1,\tau_2\rangle=K.\] 一般来说 \(K\) 是 \(G\) 的子群，但在这里 \(G\) 和 \(K\) 就是同一个群。我们不解释为什么 \(G=K\)，这里只承认这一点，然后借助这个事实来说明 \(K\) 就是 Great dodecahedron 的对称群。

首先 \(\langle \tau_1,\tau_2\rangle=\langle \rho_1,\rho_2\rangle\) 是顶点 \(A\) 的稳定化子群，所以 Great dodecahedron 和正二十面体的顶点集是一样的。但 \(\tau_1\tau_2\) 是一个角度为 144 度的旋转，这一点和 \(\rho_1\rho_2\) 是一个 72 度的旋转不同，所以 Great dodecahedron 的 vertex configure 是一个五角星，而不像正二十面体那样是一个五边形。

其次 \(\langle\tau_0,\tau_2\rangle=\langle\rho_0,\rho_2\rangle\) 为边 \(AQ\) 的稳定化子群，所以 Great dodecahedron 的边集和正二十面体也是一样的。

它俩的区别在于边组成面的方式不一样。\(\langle\tau_0,\tau_1\rangle\) 是 Great dodecahedron 面的稳定化子群，注意到 \(\tau_1\) 是关于 \(AO\) 的反射，它会把 \(AQ\) 映射为 \(AK\)，这正对应选择第 \(k\) 条边的操作。\(\tau_0\tau_1\) 是一个绕着顶点 \(O\) 的角度为 \(2\pi/5\) 的旋转，所以 \(AQ\) 在子群 \(\langle \tau_0,\tau_1\rangle\) 作用下会绕 \(O\) 转一圈，正对应 Facetting 操作得到的一个面。

我们来找出 \(\tau_0,\tau_1,\tau_2\) 之间隐藏的一条生成关系：

注意到 \(\tau_1\tau_2\tau_1=\tau_1\rho_2\tau_1\) 是关于 \(AP\) 的反射，它和 \(\tau_0=\rho_0\) 的复合是绕着 \(P\) 点角度为 \(2\pi/3\) 的旋转，所以 \((\tau_0\tau_1\tau_2\tau_1)^3=1\)。加入这个额外的生成关系得到的就是 \(K\) 的正确的表现： \[\begin{align*} K = \langle\tau_0,\tau_1,\tau_2 \ |\ &\tau_0^2=\tau_1^2=\tau_2^2=(\tau_0\tau_1)^5=(\tau_1\tau_2)^5=\\&(\tau_0\tau_2)^2=(\tau_0\tau_1\tau_2\tau_1)^3=1\rangle. \end{align*}\]

所以我们就可以对 \(K\) 照搬之前的绘制步骤了。

这个额外的生成关系其实也有背后的解释：对 Faceting 手术得到的新多面体再进行一次 Faceting 手术是可以回到原来的多面体的。对 great dodecahedron 每次沿着它的边，选择当前离开的边的右手第二个边走下去，即从 \(Q\) 走到 \(A\) 时，不是选择 \(AK\) 继续走下去，而是选择 \(AO\)，这样走下去又会得到正二十面体的三角形的面，这对应的就是额外的生成关系中的指数 3。

这一点从群上也可以得到验证。

\[K=\langle \tau_0,\tau_1,\tau_2\rangle\xrightarrow{\ \varphi_2\ }\langle\tau_0,\tau_1\tau_2\tau_1,\tau_2\rangle=\langle\rho_0,\rho_2\rho_1\rho_2,\rho_2\rangle=G.\]

关于 Faceting 手术可以在 McMullen 和 Schulte 所著的 Abstract Regular Polytopes 一书中找到。

Snub cube 的计算

如果你理解了上面的内容，snub 多面体的情形也是不难理解的。我以 snub cube 来说明：

Snub cube 和 cube 的区别在于它的对称群只包含旋转，我们已经看到 cube 的对称群 \(G\) 的表现为 \[G = \langle\rho_0,\rho_1,\rho_2\ |\ \rho_0^2=\rho_1^2=\rho_2^2=(\rho_0\rho_1)^4=(\rho_1\rho_2)^3=(\rho_0\rho_2)^2=1\rangle.\] 它有 48 个元素，其中 24 个是旋转。这些旋转可以由 \(r_0=\rho_0\rho_1, r_1=\rho_1\rho_2,r_2=\rho_0\rho_2\) 生成 （由于 \(r_0r_1=r_2\) 因此实际上可以由 \(r_0\) 和 \(r_1\) 生成）。这 24 个旋转就构成了 Snub cube 的对称群 \(\widetilde{G}\)。

不难写出 \(\widetilde{G}\) 的表现为 \[\widetilde{G}=\langle r_0,r_1\ |\ r_0^4=r_1^3=(r_0r_1)^2=1\rangle.\]

利用 Todd-Coxeter 算法不难求出这个群的所有 24 个元素：

\[\begin{array}{lll}e&r_{0}&r_{0}r_{0}\\r_{0}r_{0}r_{0}&r_{1}&r_{1}r_{1}\\r_{0}r_{1}&r_{0}r_{1}r_{1}&r_{0}r_{0}r_{1}\\r_{0}r_{0}r_{1}r_{1}&r_{0}r_{0}r_{0}r_{1}&r_{1}r_{0}\\r_{1}r_{0}r_{0}&r_{1}r_{0}r_{0}r_{0}&r_{1}r_{1}r_{0}\\r_{1}r_{1}r_{0}r_{0}&r_{0}r_{1}r_{1}r_{0}&r_{0}r_{1}r_{1}r_{0}r_{0}\\r_{0}r_{0}r_{1}r_{1}r_{0}&r_{1}r_{0}r_{0}r_{1}&r_{1}r_{0}r_{0}r_{1}r_{1}\\r_{1}r_{0}r_{0}r_{0}r_{1}&r_{1}r_{1}r_{0}r_{0}r_{1}&r_{0}r_{1}r_{1}r_{0}r_{0}r_{1}\end{array} \]

注意在 snub 的情形初始顶点 \(v_0\) 不属于任何镜面，所以其稳定化子群只有单位元 1，即每个 \(g\in\widetilde{G}\) 把 \(v_0\) 变换为不同的顶点。将它们作用在 \(v_0\) 上即得 snub cube 的所有顶点。

我们现在利用轨道—稳定化子的理论来求 snub cube 的边。snub cube 的边也是分类型的，每个 \(r_i(i=0,1,2)\) 作用在 \(v_0\) 上可得一个类型为 \(i\) 的边 \(e_i=(v_0, v_0\cdot r_i)\) ⁶，我们来定出 \(e_i\) 的稳定化子群 \(H\)。

首先注意到任何 \(g\in G\) 如果保持 \(e_i\) 不变，则只有两种可能，要么它保持 \(e_i\) 上每个点不变，要么它将 \(e_i\) 关于其中点进行翻转。这一点对 \(g\in\widetilde{G}\) 自然也成立。所以若 \(g\in\widetilde{G}\) 保持 \(e_i\) 不变，则要么 \(v_0g = v_0, v_0r_i=v_0r_ig\)，要么 \(v_0g = v_0r_i,v_0r_ig=v_0\)。前一种情形说明 \(g\) 属于 \(v_0\) 的稳定化子群从而只能是单位元；后一种情形说明 \(r_ig\) 和 \(r_ig^{-1}\) 都属于 \(v_0\) 的稳定化子群从而 \(r_ig=r_ig^{-1}=1\)，即 \(g=r_i\) 且 \(r_i^2=1\)。总之我们证明了只有在 \(r_i^2=1\) 时 \(e_i\) 才有非平凡的稳定化子群，这时稳定化子群是二阶循环群 \(\langle r_i\rangle\)。

于是 snub cube 的类型为 \(r_0\) 和 \(r_1\) 的边的个数都是 24/1=24 个；类型为 \(r_2\) 的边的个数为 24/2=12 个，从而 snub cube 总共有 24+24+12=60 条边。

snub cube 的面可以这样求：由于 \(r_0^4=1\) 所以 \(r_0\) 可以生成一个正四边形的面，类似地由于 \(r_1^3=1\) 所以 \(r_1\) 可以生成一个正三角形的面，而由于 \(r_2^2=1\) 所以 \(r_2\) 生成的面是退化的。这种由单个旋转生成的面的稳定化子群是很好求的：若 \(g\) 保持 \(r_i\) 生成的面不变，则其必然把某个形如 \(v_0r_i^k\) 的顶点变换为 \(v_0\)，即 \(g=r_i^{-k}\) 是 \(r_i\) 的某次幂，反之易见 \(r_i\) 的任何幂都保持此面不变，所以其稳定化子群即为循环群 \(\langle r_i\rangle\)。

于是 \(r_0\) 生成的面的个数为 24/4=6，\(r_1\) 生成的面的个数为 24/3=8，\(r_2\) 生成的面都退化因而个数是 0，总计 14 个面。

小心！我们还漏掉了一种三角面，它源自 \(r_0r_1=r_2\) 这个关系。考虑 \(\{v_0, v_0r_1, v_0r_2\}\) 这三个顶点，这三个顶点中 \((v_0,v_0r_1)\) 构成一条类型为 \(r_1\) 的边， \((v_0,v_0r_2)\) 构成一条类型为 \(r_2\) 的边，而 \(r_0r_1=r_2\) 这个关系告诉我们 \[(v_0, v_0r_0)\xrightarrow{\ r_1\ }(v_0r_1, v_0r_0r_1) = (v_0r_1, v_0r_2).\] 即 \((v_0r_1, v_0r_2)\) 是一条类型为 \(r_0\) 的边，它是由将 \(r_1\) 作用在类型为 \(r_0\) 的初始边 \((v_0, v_0r_0)\) 上得到的，于是 \(\{v_0, v_0r_1, v_0r_2\}\) 构成一个三角形的三个顶点，其三条边在对称群作用下属于不同的轨道，所以这个三角形的稳定化子必然保持每条边不变，从而只能是恒等元，从而这样的面有 24/1=24 个。

于是 snub cube 一共有 14+24=38 个不同的面。

这里介绍的方法也适用于其它的 snub 多面体以及 snub 24-cell。

多面体的顶点投影到 Coxeter 平面

项目中还实现了一个 draw_on_coxeter_plane(*args, **kwargs) 方法，用于绘制将多面体的顶点投影到其 Coxeter 平面上后得到的图案，例如下图显示的是将 600-cell 的 120 个顶点投影到其 Coxeter 平面上的结果：

你可以和 wikipedia 上的效果 比较一下。

附录：手算 Todd-Coxeter

对简单的群，Todd-Coxeter 算法完全可以用手算快速得出结果。我非常推荐 Borcherds 的视频，他的演示非常精彩：

仿照 Borcherds 的方法，前面正方形的例子可以很快写出来：

我来解释一下步骤：我们将画出一个有限图，图的每个顶点代表 \(H=\langle s_0,s_1\rangle\) 的一个陪集，每个顶点有三条不同颜色的边，表示此陪集在生成元 \(s_i\) 作用下的结果。

1. 首先我们在空白纸上画出第一个顶点，它对应的陪集是 \(H=H_0\) 自身。\(H\) 包含 \(s_0,s_1\)，所以红、绿边是自边。\(s_2\)，即蓝色的边，会把它映射为一个新顶点 \(H_1\)。
2. 从 \(H_0\) 出发，利用红蓝交换，可得红色保持 \(H_1\) 不动。但是绿蓝不交换，所以绿色将 \(H_1\) 映射为新顶点 \(H_2\)。
3. \((\text{绿蓝})^3=1\)，即 \(H_2\xrightarrow{(\text{绿蓝})^3}H_2\)，所以 \[H_2\xrightarrow{\text{绿}} H_1\xrightarrow{\text{蓝}} H_0\xrightarrow{\text{绿}} H_0\xrightarrow{\text{蓝}} H_1\xrightarrow{\text{绿}} H_2\xrightarrow{\text{蓝}} H_2.\] 所以蓝色保持 \(H_2\) 不动。红绿不交换，所以红色将 \(H_2\) 映射为新顶点 \(H_3\)。
4. 仿照上面的分析继续下去，可以发现到 \(H_5\) 时，三种颜色的边不会给出新顶点。所以 \(\{H_0,\ldots,H_5\}\) 就是 \(G/H\) 的全部陪集。

上一篇：静电场与 Marden 定理

下一篇：Möbius 变换的分类与上半双曲空间的等距