Schur 多项式与钩长公式
在数学中有那么一些问题，它们的表述简单而初等，但是解决起来却非常困难，往往需要相当的奇思妙想和深刻的工具。围绕这些问题。不同领域的数学相互交织，演绎出许多奇妙的故事。
Young 表就是一个典型的例子，组合数学，表示论，概率论在这里发生了奇妙的交汇。
我们从一个有趣的问题开始：
问题： \(n\) 位选民要在一次选举中给 \(m\) 个候选人投票，每个选民只能投一票。已知第 \(i\) 位候选人最终的得票数为 \(\lambda_i\)，这里 \(\sum_{i=1}^m\lambda_i=n\) 且 \(\lambda_1\geq\cdots\geq\lambda_m\)。问题是：有多少种不同的得票序列，使得在投票过程中的任一时刻，对任何的 \(i<j\)，第 \(i\) 位候选人所得的票数总不少于第 \(j\) 位候选人所得的票数？
举个例子，假设有 \(n=10\) 位选民和 \(m=4\) 个候选人，则得票序列 \[1, 2, 1, 3, 2, 1, 2, 4, 3, 1\] 表示第一个选民投票给 1 号，第二个选民投票给 2 号，第三个选民投票给 1 号，第四个选民投票给 3 号，依次类推。符合问题要求的序列必须满足对任何 \(1\leq k\leq n\) 和 \(1\leq i<j\leq m\)，序列的前 \(k\) 项中数字 \(i\) 出现的次数都大于等于数字 \(j\) 出现的次数。
虽然问题的表述很简单，但其实答案相当复杂，叫做钩长公式 (hook length formula)。钩长公式有好几个证明，但我最喜欢的证明是基于 Schur 多项式的理论，接下来就来介绍它。
Schur 多项式的组合定义
设 \(\lambda=(\lambda_1,\lambda_2,\ldots)\) 是一个非负整数构成的序列，且只有有限多个非零项。如果它满足 \(\lambda_1\geq \lambda_2\geq\cdots\)，则称 \(\lambda\) 是一个整数分拆，简称分拆，并记 \(|\lambda|=\sum\limits_{i=1}^\infty \lambda_i\)。由于 \(\lambda\) 只有有限多项非 0，\(|\lambda|\) 总是有限的。如果 \(|\lambda|=k\) 就称 \(\lambda\) 是整数 \(k\) 的分拆，记作 \(\lambda\vdash k\)。此外，记 \(l(\lambda)\) 为 \(\lambda\) 中非零项的个数。
对每个分拆 \(\lambda\vdash k\)，可以用一个图 \(F_\lambda\) 来表示它，称为 \(\lambda\) 的 Ferrers 图。\(F_\lambda\) 由 \(k\) 个方格组成，排列规则如下：第一行有 \(\lambda_1\) 个方格，第二行有 \(\lambda_2\) 个方格，. . . 以此类推，每一行都是左对齐的，总共有 \(l(\lambda)\) 行。
例如，分拆 \(\lambda=(4, 2, 2, 1)\) 的 Ferrers 图如下：
| \(\phantom{}\) | \(\phantom{}\) | \(\phantom{}\) | \(\phantom{}\) |
| \(\phantom{}\) | \(\phantom{}\) | ||
| \(\phantom{}\) | \(\phantom{}\) | ||
| \(\phantom{}\) |
注意 \(\lambda\) 中的 0 不出现在 Ferrers 图中。
将 \(F_\lambda\) 沿主对角线翻转（即行列互换），得到的也是一个 Ferrers 图，其对应的分拆称为 \(\lambda\) 的共轭分拆，记作 \(\lambda'=(\lambda_1',\lambda_2',\ldots,\lambda_r')\)，其中 \(\lambda_i'\) 是原 Ferrers 图第 \(i\) 列的长度，且 \(r=\lambda_1\)。
例如，上图转置后得到的共轭分拆为 \(\lambda'=(4, 3, 1, 1)\)：
| \(\phantom{}\) | \(\phantom{}\) | \(\phantom{}\) | \(\phantom{}\) |
| \(\phantom{}\) | \(\phantom{}\) | \(\phantom{}\) | |
| \(\phantom{}\) | |||
| \(\phantom{}\) |
在 \(F_\lambda\) 的每个方格中填入正整数，并满足以下条件：
- 每一行从左到右非递减；
- 每一列从上到下严格递增。
满足上述条件的表格称为半标准 Young 表 (semistandard Young tableaux)，简称为 SSYT；如果一个 SSYT 的所有填入的数字恰好为 \(\{1,2,\ldots,n\}\)，且每个数字只出现一次，则称其为一个标准 Young 表 (standard Young tableaux)，简称为 SYT。
例： 下图分别显示的是形状为 \(\lambda=(4, 3, 2,1)\) 的一个半标准和一个标准 Young 表。
| 1 | 1 | 2 | 2 |
| 3 | 3 | 8 | |
| 4 | 6 | ||
| 5 |
| 1 | 3 | 6 | 10 |
| 2 | 5 | 7 | |
| 4 | 9 | ||
| 8 |
用记号 \({\rm SSYT}(n,\lambda)\) 表示所有形状为 \(\lambda\)，并且填入的数字不超过 \(n\) 的半标准 Young 表组成的集合。显然若要使得此集合非空必须有 \(n\geq l(\lambda)\)（SSYT 从上到下是递增的，第一列的最后一行填入的整数至少是 \(l(\lambda)\)）。当 \(|\lambda|=n\) 时我们也将其简写为 \({\rm SSYT}(\lambda)\)。类似地，\({\rm SYT}(\lambda)\) 表示所有形状为 \(\lambda\) 的标准 Young 表的集合。
文章开头的投票序列问题本质上等价于计算集合 \({\rm SYT}(\lambda)\) 的大小。具体来说，每个符合要求的投票序列都可以唯一地转化为一个标准 Young 表，方法如下：
- 依次处理数字 \(j=1,2,\ldots,n\)，如果选民 \(j\) 将票投给了候选人 \(i\)，则将数字 \(j\) 填入 \(\lambda\) 的 Ferrers 图的第 \(i\) 行从左边数起第一个空着的方格中。
- 所有 \(n\) 个数字填写完后得到的就是一个标准 Young 表 \(T\)。若不然，假设第 \(k\) 个选民投票给第 \(j\) 个候选人，导致候选人 \(j\) 的得票数大于某个候选人 \(i\,(i<j)\) 时，第 \(j\) 行填入的 \(k\) 上方对应的第 \(i\) 行的方格此时是空的，这个方格未来只能填大于 \(k\) 的数字，这样的 Young 表当然不是标准的。
反之对一个标准 Young 表，其所有 \(\leq k\) 的方格构成一个子 Young 表 \(T_k\)，其每行长度是投票截止到第 \(k\) 个选民时，第 \(i\) 个候选人的得票数，所以它给出一个满足要求的投票序列。
例： 标准 Young 表
| 1 | 3 | 6 | 10 |
| 2 | 5 | 7 | |
| 4 | 9 | ||
| 8 |
对应的得票序列为 \[1, 2, 1, 3, 2, 1, 2, 4, 3, 1\] 只要依次将 \(1,2,\ldots,10\) 所在的行写出来即可。
为了解决 \({\rm SYT}(\lambda)\) 的计数问题，我们需要引入 Schur 多项式的概念，Schur 多项式可以看作是半标准 Young 表的“生成函数”。
给定一个满足 \(n\geq l(\lambda)\) 的分拆 \(\lambda=(\lambda_1,\ldots,\lambda_n)\) （允许某些 \(\lambda_i\) 为零），\(T\in {\rm SSYT}(n,\lambda)\) 是半标准 Young 表。我们称 \(c(T)=(c_1,c_2,\ldots,c_n)\) 为 \(T\) 的容度 (content)，其中 \(c_i\) 是 \(T\) 中数字 \(i\) 出现的次数。记 \[X^{c(T)} = x_1^{c_1}x_2^{c_2}\cdots x_n^{c_n}.\] \(X^{c(T)}\) 是一个单项式。
例： 对 \(n=10\) 和 \(\lambda=(4,3,2,1)\)，上面的半标准 Young 表
| 1 | 1 | 2 | 2 |
| 3 | 3 | 8 | |
| 4 | 6 | ||
| 5 |
的容度为 \((2, 2, 2, 1, 1, 1, 0, 1, 0, 0)\)，其对应的单项式为 \[X^{c(T)} = x_1^2x_2^2x_3^2x_4x_5x_6x_8.\]
Schur 多项式的组合定义. 设 \(n\) 是一个正整数，\(\lambda=(\lambda_1,\ldots,\lambda_n)\) 是一个满足 \(n\geq l(\lambda)\) 的分拆 （允许某些 \(\lambda_i\) 为零），定义 \(n\) 变元多项式 \[s_\lambda(x_1,\ldots,x_n)=\sum_{T\in {\rm SSYT}(n,\lambda)}X^{c(T)}.\] \(s_\lambda\) 叫做 \(n\) 变元的 Schur 多项式。
注意 \(s_\lambda(x_1,\ldots,x_n)\) 只有在 \(l(\lambda)\leq n\) 时才有定义。
例： 对 \(\lambda=(3,2)\)， \[\begin{align*}s_{(3,2)}(x_1,x_2,x_3) \,= \, & x_1^3x_2^2 + x_1^3x_3^2 + x_1^3x_2x_3 + x_1^2x_2^3 + x_1^2x_3^3 + 2x_1^2x_2x_3^2 + \\ &2x_1^2x_2^2x_3 +x_1x_2x_3^3 + 2x_1x_2^2x_3^2 + x_1x_2^3x_3 + x_2^2x_3^3 + x_2^3x_3^2. \end{align*}\] 前几项对应的半标准 Young 表如下：
| \(x_1^3x_2^2\) | \(x_1^3x_3^2\) | \(x_1^3x_2x_3\) | \(x_1^2x_2^3\) | \(x_1^2x_3^3\) | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
可以看到虽然 Schur 多项式的定义很直观，但写出它的具体表达式来却并不容易。我们需要找到 Schur 多项式的其它表现形式。首先我们将证明 Schur 多项式总是对称多项式。
Bender-Knuth 对合
这一节我们来证明 Schur 多项式 \(s_\lambda(x_1,\ldots,x_n)\) 是对称多项式。即它在交换任何两个变元 \(x_i\) 和 \(x_j\) 后保持不变。为此只要证明它在交换 \(x_i\) 和 \(x_{i+1}\) 后保持不变即可。而这又只要说明容度为 \((\ldots,c_i,c_{i+1},\ldots)\) 的半标准 Young 表与容度为 \((\ldots,c_{i+1},c_i,\ldots)\) 的半标准 Young 表之间存在一一对应。看起来只要对每个形状为 \(\lambda\) 的半标准 Young 表，把其中的数字 \(i\) 全换成 \(i+1\)，同时把 \(i+1\) 全换成 \(i\) 就可以了，是吗？
问题出在这样简单粗暴地修改得到的未必还是半标准的 Young 表。我们需要仔细点选择那些翻转的方格。我们作如下规定：
- 如果某个 \(i\) 的下方恰好是 \(i+1\)，就称这样的 \(i\) 和 \(i+1\) 构成匹配。
- 那些下方没有 \(i+1\) 的 \(i\)，或者上方没有 \(i\) 的 \(i+1\) 统称为未匹配的。
下图中演示了 \(i=2\) 的例子，绿色显示了匹配的元素，红色显示了未匹配的元素。
| 1 | 1 | 1 | 1 | 1 | 1 | 2 |
| 2 | 2 | 2 | 2 | 3 | 3 | 3 |
| 3 | 4 | 4 | ||||
| 4 |
关键观察：
在任意一行中，未匹配的元素总是构成一段连续的序列。即设 \(i=x\leq y\leq i+1\) 是两个未匹配的元素，则它们中间不可能有匹配的元素。
设某一行中的未匹配元素形如：\(r\) 个 \(i\) 紧接着 \(s\) 个 \(i+1\)，我们将其替换为 \(s\) 个 \(i\) 紧接着 \(r\) 个 \(i+1\)，保持其他部分不变。对 Young 表的每一行都执行这一操作，得到新表 \(T^\ast\)，此时 \(T^\ast\) 仍然是一个合法的半标准 Young 表。
例如在上面的 \(T\) 中，红色标注的未匹配的元素是 3 个 2 后面跟了 2 个 3，变换后在 \(T^\ast\) 中变成了 2 个 2 后面跟了 3 个 3：
| 1 | 1 | 1 | 1 | 1 | 1 | 2 |
| 2 | 2 | 2 | 3 | 3 | 3 | 3 |
| 3 | 4 | 4 | ||||
| 4 |
容易验证 \(T^\ast\) 的容度为 \((\ldots,c_{i+1},c_i,\ldots)\)。这个变换显然是个对合：\((T^\ast)^\ast=T\)，这就证明了 Schur 多项式是对称的。
Jacobi-Trudi 恒等式
除了通过半标准 Young 表的生成函数定义之外，Schur 多项式还有许多等价的表达方式。本节中，我们将 Schur 多项式表示为齐次对称多项式行列式的形式。
定义 3.1. 记 \(h_k(x_1,\ldots,x_n)\) 为所有次数为 \(k\) 的单项式之和： \[h_k(x_1,\ldots,x_n)=\sum_{\begin{subarray}{c}\alpha_1+\alpha_2+\cdots+\alpha_n=k\\\alpha_i\in\mathbb{Z}_{\geq0}\end{subarray}} x_1^{\alpha_1}x_2^{\alpha_2}\cdots x_n^{\alpha_n}.\] 约定 \(h_0=1\)，\(k<0\) 时 \(h_{k}=0\)。\(h_k\) 也是对称多项式，称为齐次对称多项式。
例： \(h_2(x_1,\ldots,x_n)=\sum_{i=1}^n x_n^2 + \sum_{1<i<j<n}x_ix_j\)。
Jacobi-Trudi 恒等式.
设 \(\lambda=(\lambda_1,\ldots,\lambda_n)\in\mathbb{Z}^n_{\geq0}\) 为一个分拆，则 \[s_\lambda(x_1,x_2,\ldots,x_n)=\det\left( h_{\lambda_i-i+j}\right)_{1\leq i,j\leq n}.\]
注： 另一种常见写法是 \[s_\lambda(x_1,x_2,\ldots,x_n)=\det\left( h_{\lambda_i-i+j}\right)_{1\leq i,j\leq l(\lambda)}.\] 这没有区别。实际上令 \(r=l(\lambda)\)，则 \[\det\left(h_{\lambda_i-i+j}\right)_{1\leq i,j\leq n}= \det\left(\begin{array}{cc} \begin{array}{l} h_{\lambda_1}&h_{\lambda_1+1} &\cdots & h_{\lambda_1+r-1}\\ h_{\lambda_2-1}&h_{\lambda_2} &\cdots & h_{\lambda_2+r-2}\\ & & \cdots & \\ h_{\lambda_r-(r-1)}&h_{\lambda_r-(r-2)}&\cdots & h_{\lambda_r} \end{array} & \Large\ast \\ \Large 0 & \begin{matrix}1&&\\&\ddots&\\&&1\end{matrix}\end{array}\right). \] 显然它等于左上角的主子式。
证明要用到 Gessel-Viennot 的不相交格点路径组方法。关于这个方法你可以参考我之前的 一篇博文。当然 (Martin Aigner and Ziegler 2018) 中格点路径组一章也是极好的介绍。
关键是要把每个半标准 Young 表对应到一个不相交的路径组。
下面的动图显示了 \(n=6, \lambda=(5,4,3,2,0, 0)\) 时的一个形状为 \(\lambda\) 的 Young 表 \(T\) 与其不相交的路径组：
| 1 | 1 | 1 | 1 | 2 |
| 2 | 2 | 3 | 3 | |
| 3 | 4 | 4 | ||
| 4 | 5 |
其中，\(T\) 的每一行是一个长度为 \(\lambda_i\) 的递增数列，该数列对应一条从 \((0,1)\) 到 \((\lambda_i,n)\) 的 Gauss 路径，即这一行的“台阶图”。
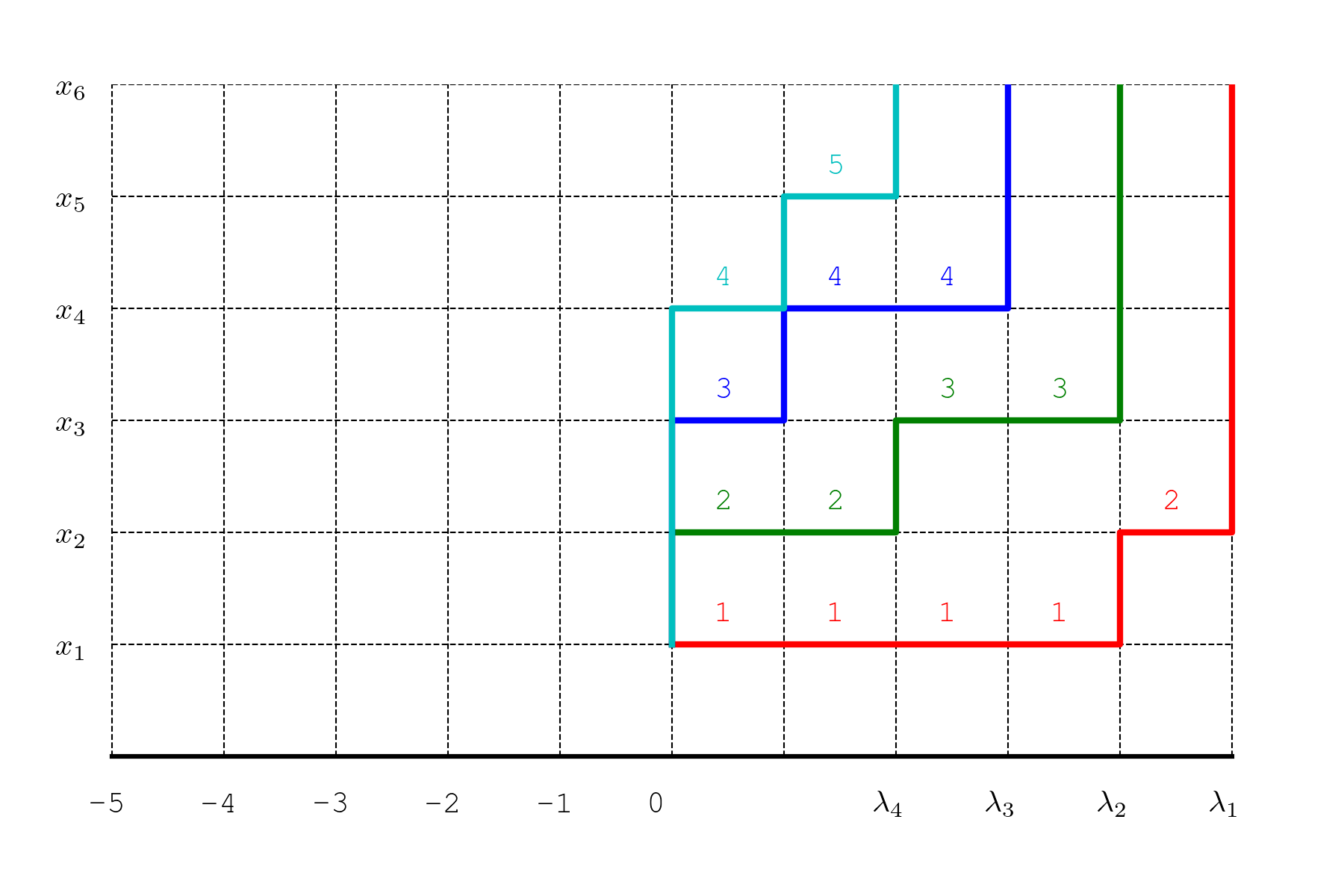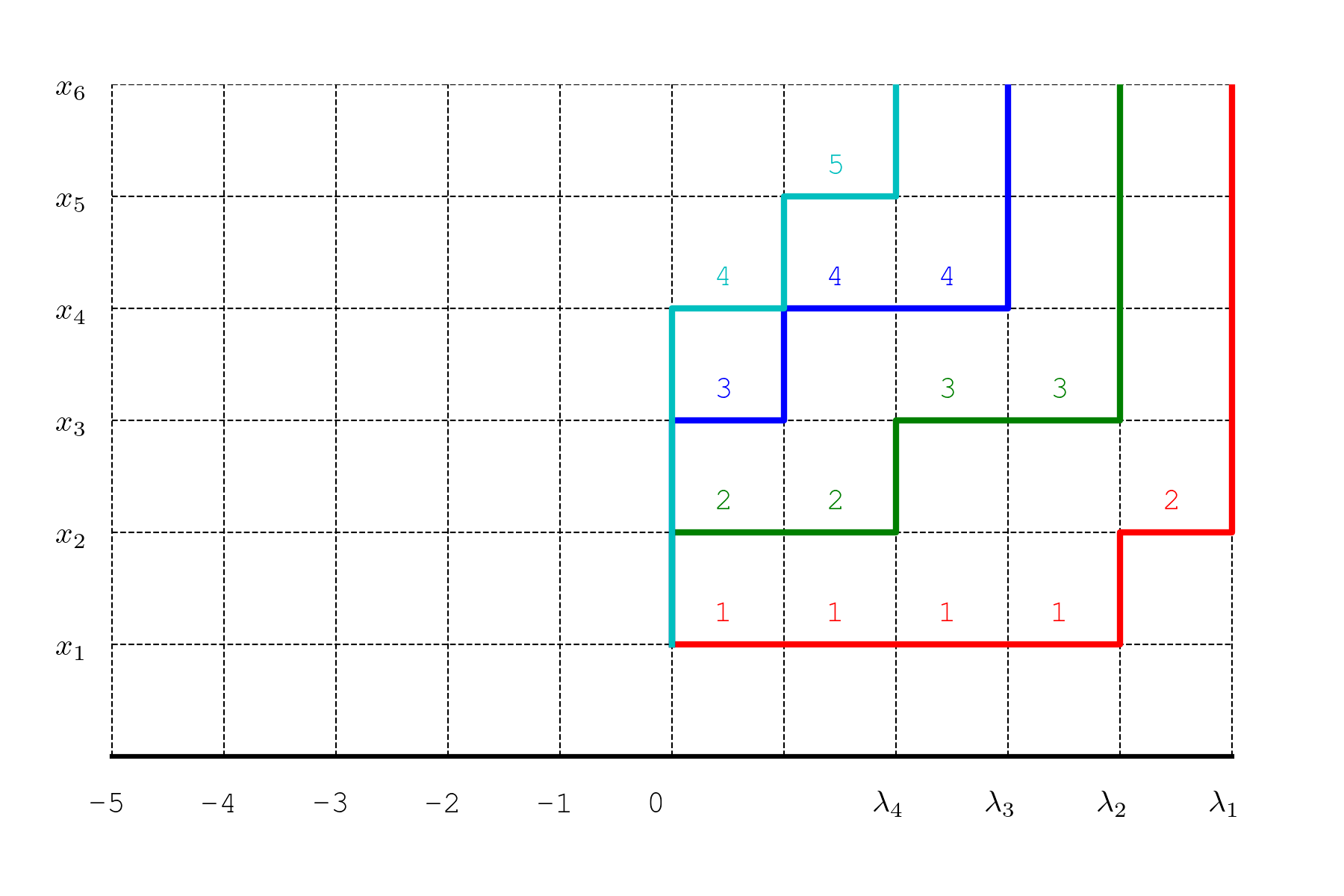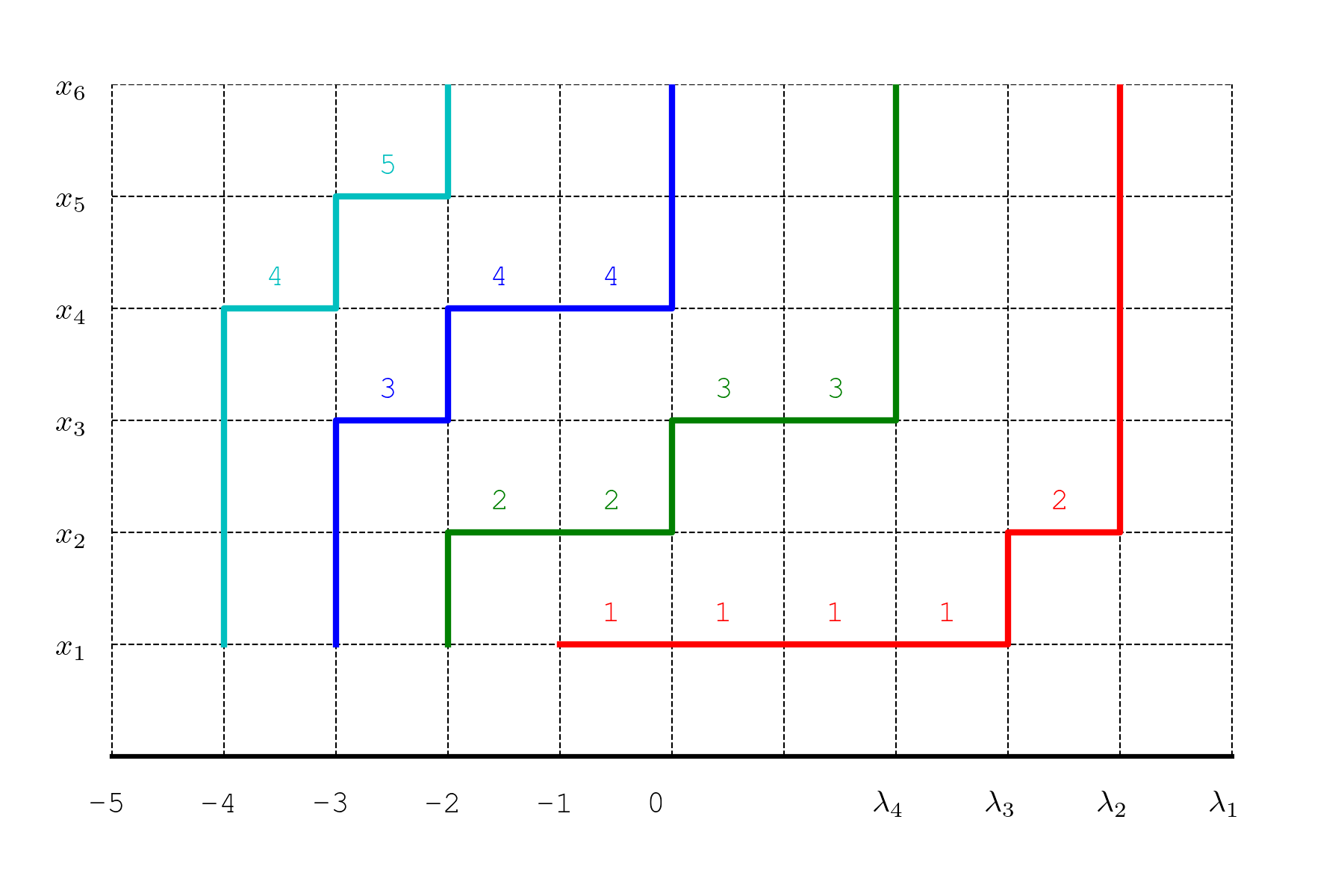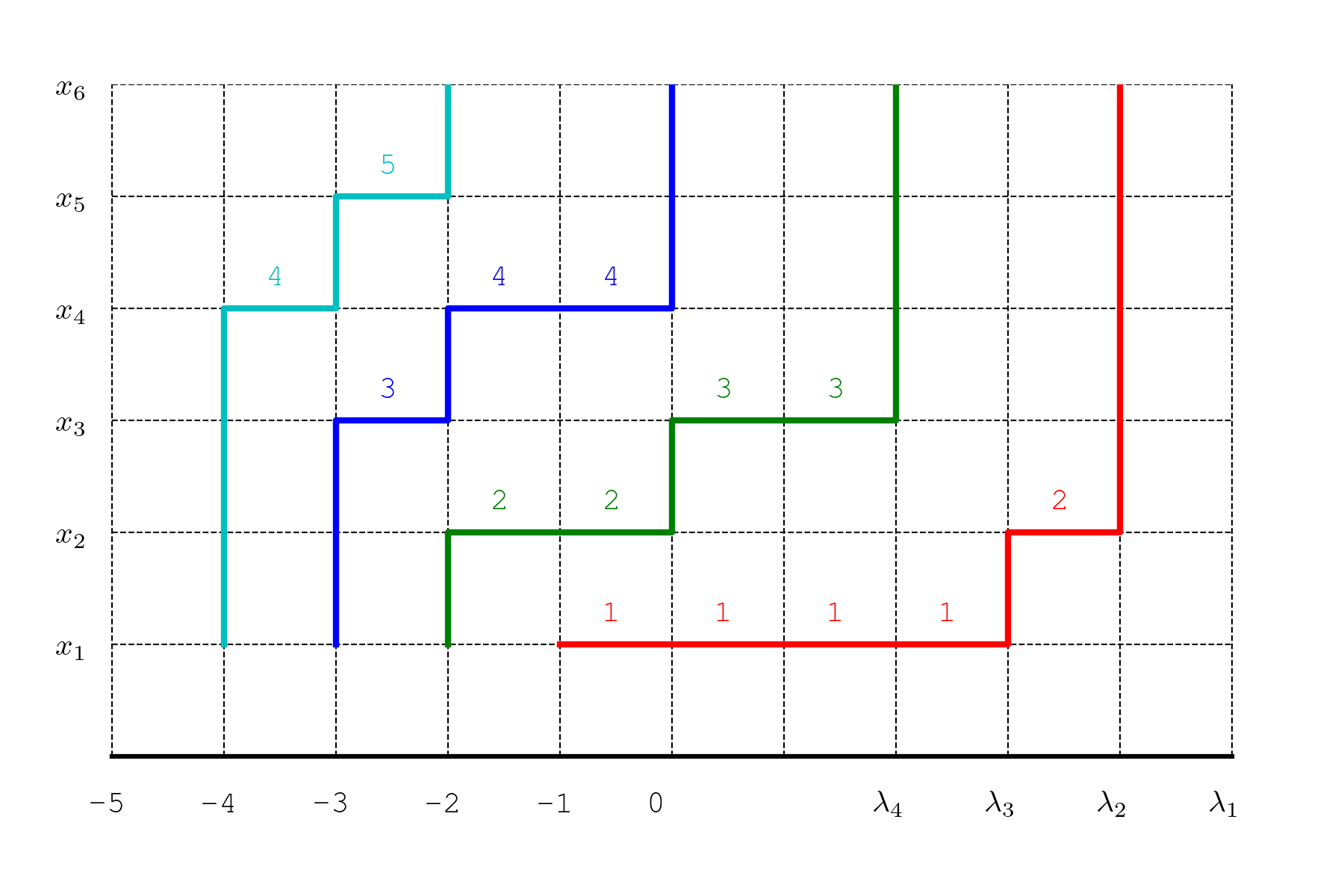
我省略了 \(\lambda_i=0\) 的部分，它们对应的是权重为 1 的垂直路径，对路径组的权重没有贡献：
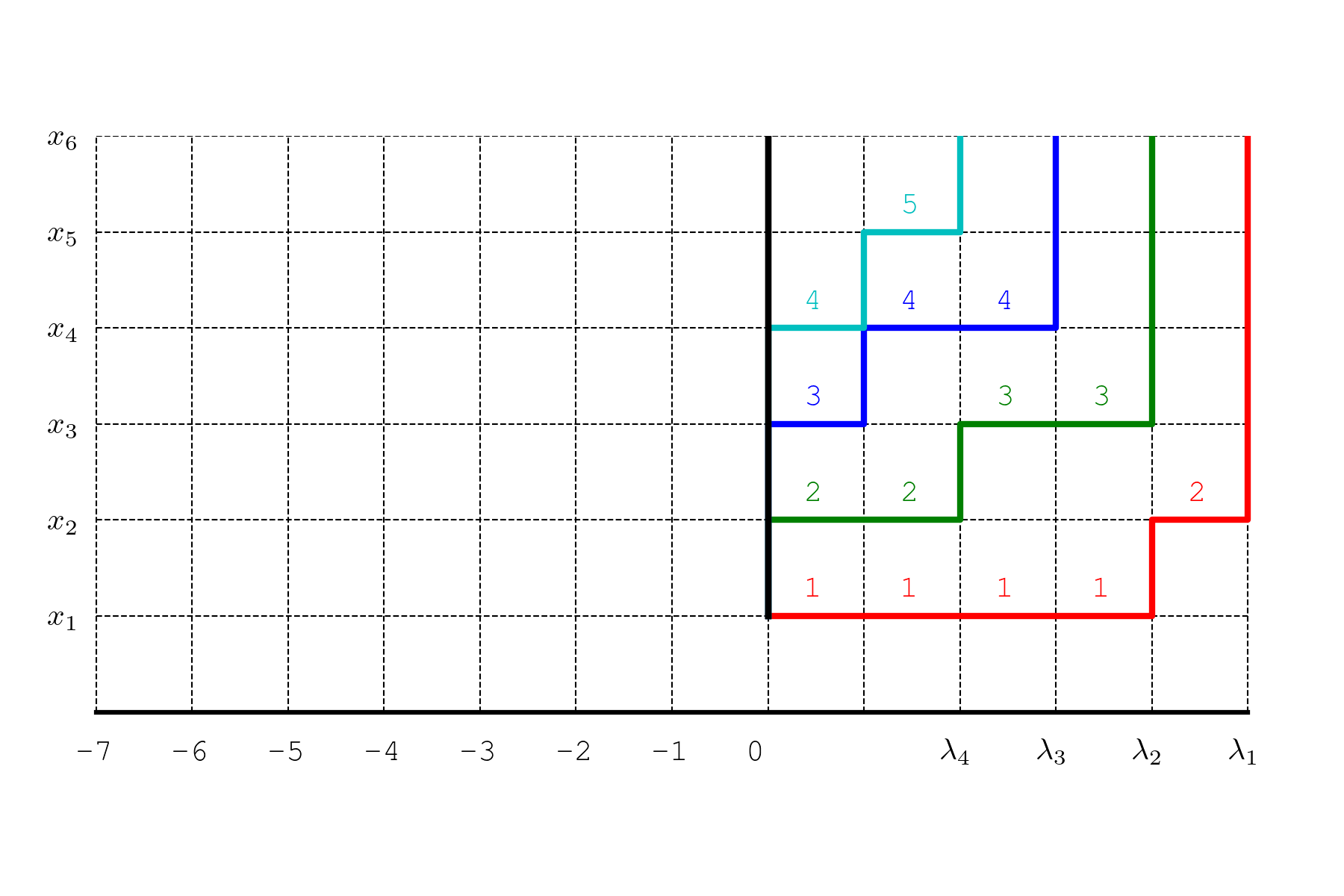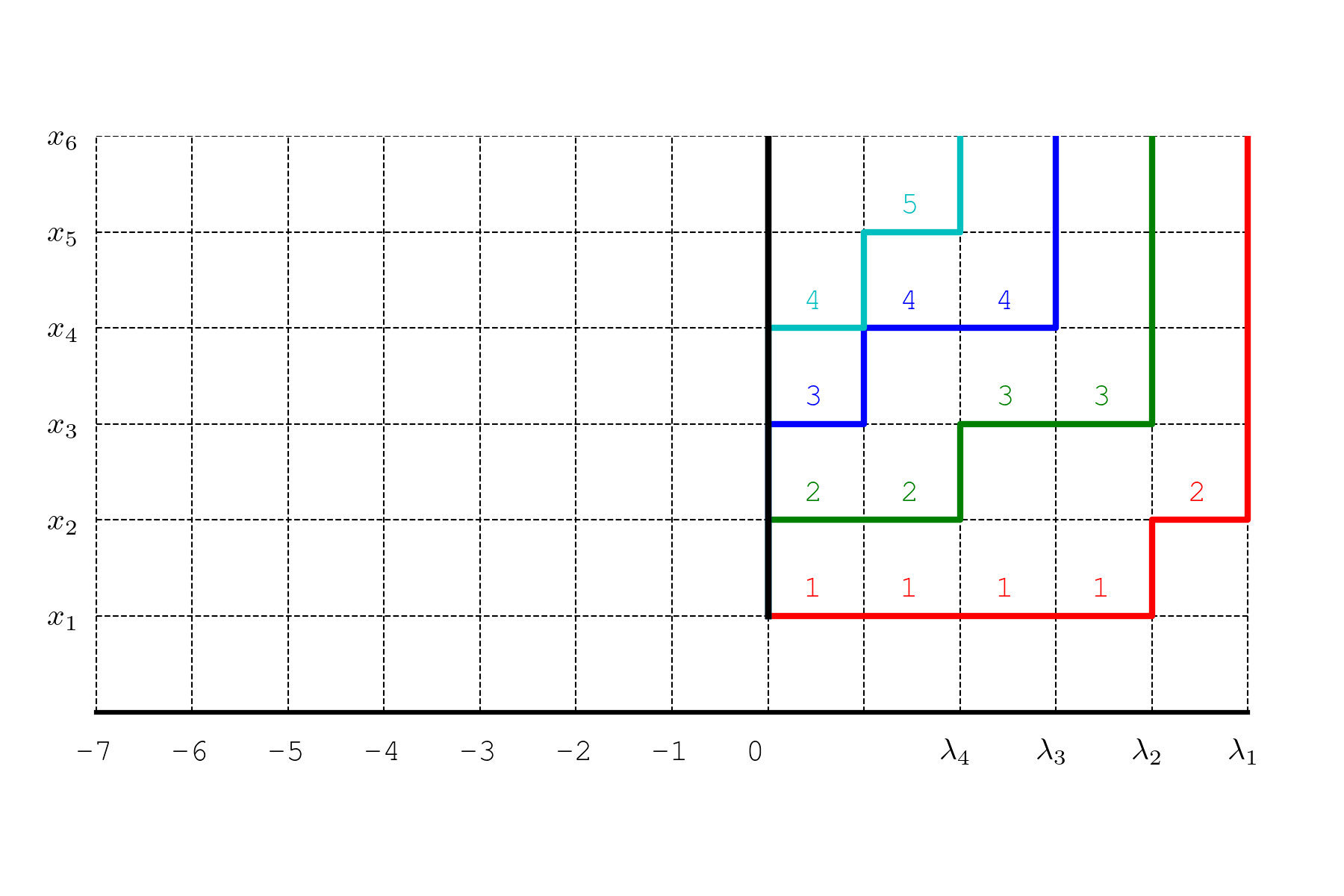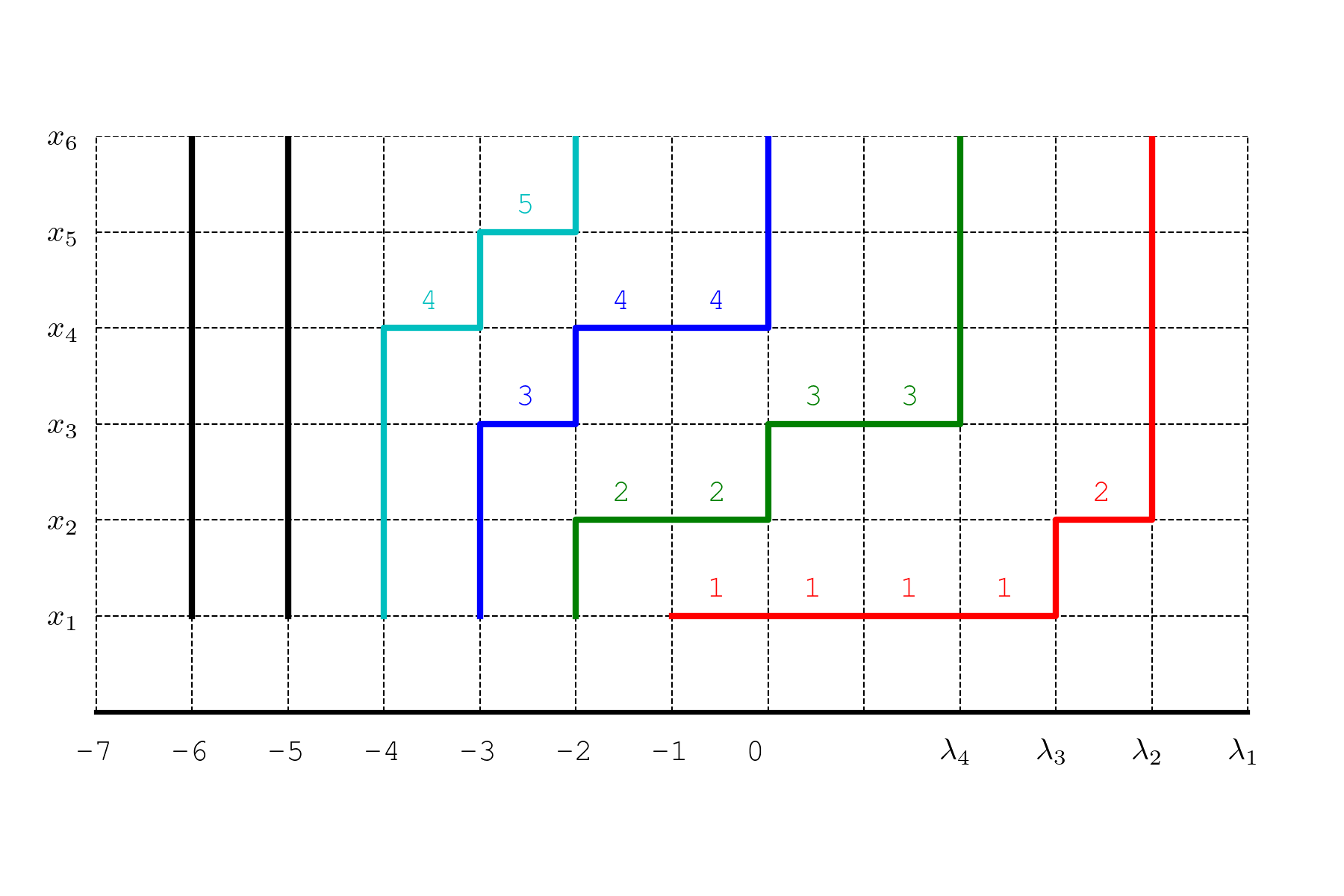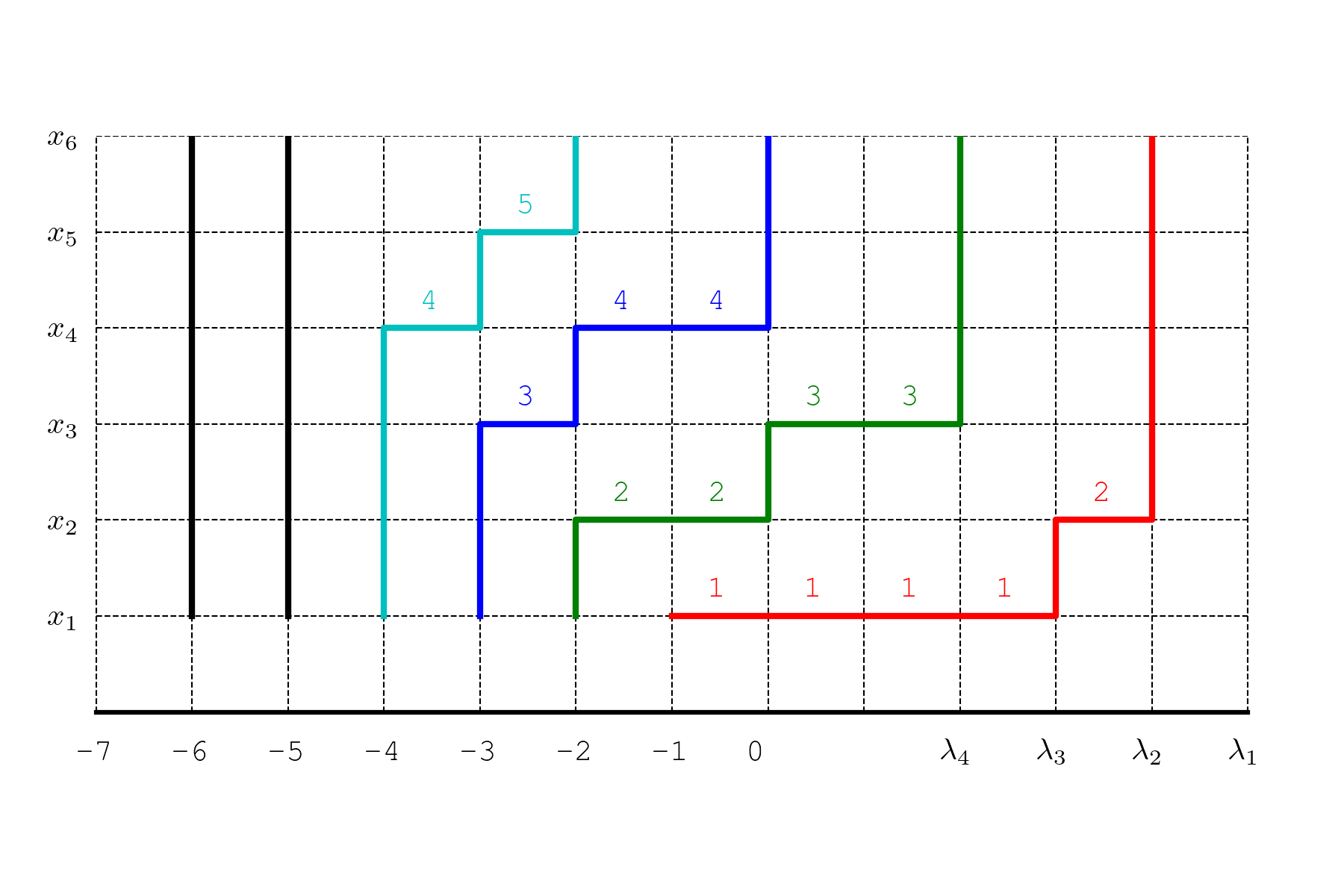
但是半标准 Young 表的列是严格递增的，这个递减关系反映在 Gauss 路径上，就是 \(T\) 的第二行对应的路径应该整体位于第一行对应路径的上方，第三行对应的路径整体位于第二行对应的路径的上方，…，两条路径之间可以有垂直的公共边，但是不能有水平的公共边。
对每个 \(i\)，将第 \(i\) 行对应的路径水平地向左平移 \(i\) 个单位，使其成为一条从 \(A_i=(-i,1)\) 到 \(B_i=(-i+\lambda_i,n)\) 的 Gauss 路径，则这样得到的 \(n\) 条路径构成一个不相交的路径组。
反过来每一个这样的不相交的路径组也对应于一个半标准 Young 表。
令水平线 \(y=k\) 的权值为 \(x_k\)，垂直边的权值一律为 1，每条路径的权重是其所含各边的权重乘积。不难验证从 \(A_j=(-j,1)\) 到 \(B_i=(-i+\lambda_i,n)\) 的所有 Gauss 路径权重之和是齐次对称多项式 \(h_{\lambda_i-i+j}\)。于是由 Gessel-Viennot 引理，行列式 \(\det\left(h_{\lambda_i-i+j}\right)_{1\leq i,j\leq n}\) 给出了所有不相交路径组的权重之和。另一方面每个不相交路径组的权重正是它对应 Young 表的权重 \(X^{c(T)}\)，所以 \[s_\lambda=\det\left(h_{\lambda_i-i+j}\right)_{1\leq i,j\leq n}.\] 这就证明了 Jacobi-Trudi 恒等式。
钩长公式
在完成前面的准备工作后，我们现在可以正式介绍钩长公式及其证明。
定义 4.1. 设 \(\lambda\vdash n\)，\(F_\lambda\) 是其 Ferrers 图，记 \(v=(i,j)\) 为 \(F_\lambda\) 中第 \(i\) 行第 \(j\) 列位置的方格 （只考虑那些有方格的位置）。我们计算那些与 \(v\) 同行但是位置在 \(v\) 的右边，以及与 \(v\) 同列但是位置在 \(v\) 的下方的方格的总数，\(v\) 自己也算一个但是只算一次。这个数字称作 \(v\) 的钩子长度，记作 \(h_v\)。
例如 \(\lambda=(5, 4, 3, 2, 1)\) 的 Ferrers 图中，\(v=(1, 1)\) 的钩子长度 \(h_v=5\)。
| \(\phantom{}\) | \(\phantom{}\) | \(\phantom{}\) | \(\phantom{}\) | \(\phantom{\bullet}\) |
| \(\phantom{\bullet}\) | \(\bullet\) | \(\bullet\) | \(\bullet\) | |
| \(\phantom{\bullet}\) | \(\bullet\) | |||
| \(\phantom{\bullet}\) | \(\bullet\) | |||
| \(\phantom{\bullet}\) |
一般地，\((i,j)\) 位置的方格的 hook 长度为 \(\lambda_i + \lambda'_j - i - j + 1\)。
Hook
length formula.
形状为 \(\lambda\) 的标准 Young 表的个数由以下公式给出： \[|{\rm SYT}(\lambda)|=f_\lambda=\frac{n!}{\prod\limits_{v\in F_\lambda}h_v}.\]
引理 4.2. 设 \(\mu_i=\lambda_i+r-i\)，这里 \(r=l(\lambda)=\lambda_1',\,1\leq i\leq r\)，则 \[\prod_{v\in F_\lambda} h_v =\frac{\prod\limits_{i=1}^r \mu_i!}{\prod\limits_{i<j}(\mu_i-\mu_j)}.\]
注意 \(\mu_i=h_{i1}\) 正是第 1 列第 \(i\) 行方格的钩子长度。
引理 4.2 的结论可以很容易由下面的 引理 4.3 得出：
引理 4.3. 对固定的 \(1\leq k\leq r\)，\(F_\lambda\) 的第 \(k\) 行所有方格的钩子长度集合 \(\{h_{kj},1\leq j\leq\lambda_k\}\) 与 \(\{\mu_k-\mu_i, k\leq i\leq r\}\) 不相交，且它们的并集恰好构成 \(\{0,1,\ldots,\mu_k\}\)。因此，第 \(k\) 行所有方格的钩子长度的乘积为 \[\prod_{j=1}^{\lambda_k}h_{kj}=\frac{\mu_k!}{\prod\limits_{k<i}(\mu_k-\mu_i)}.\]
引理 4.3 的证明：这里的证明改编自 Macdonald (2008)。
我们从 \(F_\lambda\) 的左下角开始，沿着边界，每一步向右或者向上行走，直到第 \(k\) 行最右边的方格右上角为止，总共要走 \(h_{k1}+1\) 步。将经过的边依次标号为 \(0,1,\ldots,h_{k1}\)。
不难看出：
- 所有竖直边的标号构成集合 \(\{h_{i1} \mid k\leq i\leq r\}\)，即图中第一列方格的钩子长度。
- 所有水平边的标号构成集合 \(\{h_{k1} - h_{kj}\mid 1\leq j\leq\lambda_k\}\)。即 \(h_{k1}\) 减去图中第一行（也是原 \(F_\lambda\) 的第 \(k\) 行）方格的钩子长度。
于是我们有不交并 \[\{0,1,\ldots,h_{k1}\}=\{h_{i1} \mid k\leq i\leq r\}\sqcup \{h_{k1} - h_{kj}\mid 1\leq j\leq\lambda_k\}.\] 同时用 \(h_{k1}\) 减去两边的集合，得到不交并 \[\{0,1,\ldots,h_{k1}\}=\{h_{k1}-h_{i1} \mid k\leq i\leq r\}\sqcup \{h_{kj}\mid 1\leq j\leq\lambda_k\}.\]
前者正是集合 \(\{\mu_k-\mu_i\mid k\leq i\leq r\}\)，这就证明了 引理 4.3。\(\blacksquare\)
最后我们来完成钩长公式的证明：这里使用了一个小技巧：考虑关于无穷多个变元的对称多项式环 \(\Lambda[x_1,\ldots,x_n,\ldots]\)，任何 \(k\) 变元的 Schur 多项式都是 \(\Lambda\) 中的元素。\(\Lambda\) 到有理数域上的单变元形式幂级数环 \(\mathbb{Q}[t]\) 有一个同态 \(\theta\)： \[\theta(f) = \sum_{k=0}^\infty f_k \frac{t^k}{k!}.\] 其中 \(f_k\) 是 \(f\) 中单项式 \(x_1x_2\cdots x_k\) 的系数。不难验证 \(\theta\) 是 \(\Lambda\to \mathbb{Q}[t]\) 的代数同态 1。
在齐次对称多项式 \(h_k\) 中，其形如 \(x_1x_2\cdots x_n\) 的项只有一个，就是 \(x_1x_2\cdots x_k\)，并且这一项的系数是 1，所以 \(\theta(h_k)=\frac{t^k}{k!}\)。
我们再来分析 \(\theta\) 作用在 \(n\) 变元 Schur 多项式上的结果 \(\theta(s_\lambda(x_1,\ldots,x_n))\)。这里我们要求 \(\lambda\) 满足 \(|\lambda|=n\)，即 \(\lambda\) 的 Ferrers 图恰好包含 \(n\) 个方格。单项式 \(x_1x_2\cdots x_k\) 在 \(s_\lambda(x_1,\ldots,x_n)\) 中的系数等于每个数字 \(\{1,2,\ldots,k\}\) 都恰好使用一次的不同填法的个数，这只能是 \(k=n\) 且得到的是标准 Young 表，这样的填法有 \(f_\lambda\) 种，所以 \[\theta(s_\lambda(x_1,\ldots,x_n))=f_\lambda \frac{t^n}{n!}.\]
在 Jacobi-Trudi 恒等式两边同时用 \(\theta\) 作用，得到 \[f_\lambda \frac{t^n}{n!}=\det\left( \frac{t^{\lambda_i-i+j}}{(\lambda_i-i+j)!} \right).\] 取 \(t=1\) 代入得 \[f_\lambda = n!\cdot \det\left(\frac{1}{(\lambda_i-i+j)!}\right).\] 我们把这个行列式写出来： \[f_\lambda = n!\cdot \det\begin{pmatrix} \frac{1}{\lambda_1!} & \frac{1}{(\lambda_1+1)!} & \cdots & \frac{1}{(\lambda_1+r-1)!}\\ \frac{1}{(\lambda_2-1)!} & \frac{1}{\lambda_2!} & \cdots & \frac{1}{(\lambda_2+r-2)!}\\ \cdots & \cdots &\cdots&\cdots\\ \frac{1}{(\lambda_r-r+1)!} & \frac{1}{(\lambda_r-r+2)!} & \cdots & \frac{1}{\lambda_r!} \end{pmatrix}.\] 它的最后一列恰好是 \(\{\mu_i!\mid 1\leq i\leq r\}\)，提出来以后得到 \[f_\lambda = \frac{n!}{\prod\limits_{i=1}^r\mu_i!}\cdot \det\begin{pmatrix} \mu_1^{\underline{r-1}}& \mu_1^{\underline{r-2}} & \cdots & \mu_1^{\underline{0}}\\ \mu_2^{\underline{r-1}} & \mu_2^{\underline{r-2}} & \cdots & \mu_2^{\underline{0}}\\ \cdots & \cdots &\cdots&\cdots\\ \mu_r^{\underline{r-1}}& \mu_r^{\underline{r-2}} & \cdots & \mu_r^{\underline{0}} \end{pmatrix}= \frac{n!}{\prod\limits_{i=1}^r\mu_i!}\cdot\det(\mu_i^{\underline{r-j}}).\] 其中采用了类似 M. Aigner (2007) 中的记号 \[x^{\underline{k}}=x(x-1)\cdots(x-k+1).\]
不难证明 \(\det(\mu_i^{\underline{r-j}})\) 这个行列式与 Vandermonde 行列式 \(\det(\mu_i^{r-j})\) 的值是一样的，都等于 \(\prod\limits_{i<j}(\mu_i-\mu_j)\) 2。于是 \[f_\lambda = \frac{n!}{\prod\limits_{i=1}^r\mu_i!}\cdot\prod\limits_{i<j}(\mu_i-\mu_j) = \frac{n!}{\prod\limits_{v\in F_\lambda}h_v}.\] 这就完成了钩长公式的证明。