三质点弹簧系统的简正模式
今天的问题是群表示论在物理中的一个小应用：
问题： 平面上有三个质量均为 \(m\) 的质点 \(A,B,C\)，它们位于正三角形的三个顶点。质点之间两两由弹簧相连，三个弹簧完全一样。弹簧质量忽略不计。
初始时所有质点都处于静止状态，弹簧之间没有张力。假设给这三个质点分别施加一个初始速度，使这三个质点在平面内作刚体运动，不考虑任何摩擦力和空气阻力，那么这个系统的简正模式 (normal mode) 是什么？
这里 简正模式 的含义是所有质点按照一个共同的频率和固定的相位关系相对于各自的平衡位置作简谐振动。
比较容易发现的简正模式有：
平移。初始时给所有质点以同样的速度，它们会继续以相同的速度移动。
旋转。初始时给所有质点以相同的切向速度，它们会继续绕中心旋转。
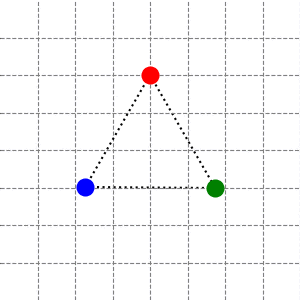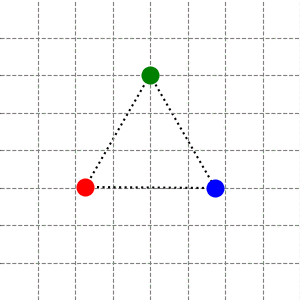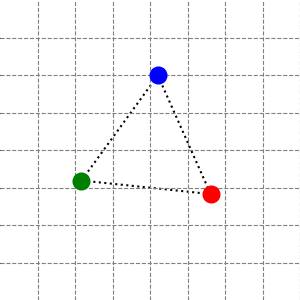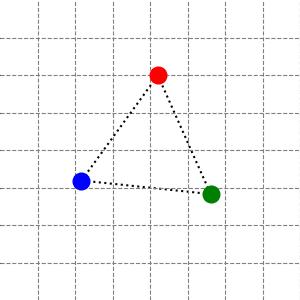
呼吸。初始时给每个质点相同的径向速度，系统会重复膨胀 — 收缩的过程。
但是要找出其它的简正模式，并保证没有遗漏，就不能只靠想象了。
我们把这个物理问题转换为一个线性代数问题，然后用一些群表示论的知识解决它。
这个质点弹簧系统有 6 个自由度 \(\{q_1,\ldots,q_6\}\)，其中 \((q_1,q_2)\)，\((q_3,q_4)\)，\((q_5,q_6)\) 分别是质点 \(A,B,C\) 在 \(x,y\) 方向上相对于其平衡位置的位移，如下图所示：
设弹簧的弹性系数为 \(k\)，原点在三角形中心，\(x\) 轴水平向右，于是三个弹簧所含的弹性势能为 （将形变投影到弹簧所在的方向） \[ \begin{align*} V=&\frac{1}{2}k(q_3-q_1)^2+\frac{1}{2}k\left[\frac{-1}{2}(q_5-q_3) + \frac{\sqrt{3}}{2}(q_6-q_4)\right]^2+\\&\frac{1}{2}k\left[\frac{1}{2}(q_1-q_5) + \frac{\sqrt{3}}{2}(q_2-q_6)\right]^2. \end{align*} \] 这是一个关于 \(\mathbf{q}=(q_1,q_2,\ldots,q_6)^T\) 的二次型： \[V =\frac{1}{2}k\,\mathbf{q}^TU\mathbf{q}.\] 其中 \[U=\frac{1}{4}\begin{pmatrix}5&\sqrt{3}&-4&0&-1&-\sqrt{3}\\ \sqrt{3}&3&0&0&-\sqrt{3}&3\\ -4&0&5&-\sqrt{3}&-1&\sqrt{3}\\ 0&0&-\sqrt{3}&3&\sqrt{3}&-3\\ -1&-\sqrt{3}&-1&\sqrt{3}&2&0\\ -\sqrt{3}&-3&\sqrt{3}&-3&0&6 \end{pmatrix}.\]
由牛顿第二定律我们有 \[m\frac{\mathrm{d}^2q_i}{\mathrm{d}t^2}=-\frac{\partial V}{\partial q_i}=-k\sum_{j=1}^6U_{ij}q_j.\] 系统的简正模式就是所有 \(q_i\) 按照同一个频率 \(\omega\) 作简谐振动，但振幅可以不同，故而可以设 \(q_i=\overline{q}_i\mathrm{e}^{i\omega t}\)，其中 \(\overline{q}_i\) 是振幅，与时间 \(t\) 无关。代入上式得到 \[\frac{m\omega^2}{k}\overline{q}_i = \sum_{j=1}^6U_{ij}\overline{q}_j.\] 即 \(U\overline{\mathbf{q}}=\lambda\overline{\mathbf{q}}\)，\(\lambda=m\omega^2/k\)，于是简正模式的振幅 \(\overline{\mathbf{q}}=(\overline{q}_1,\overline{q}_2,\ldots,\overline{q}_6)\) 是 \(U\) 的特征向量，频率可以从特征值 \(\lambda\) 得出，从而问题转化为求矩阵 \(U\) 的特征值和特征向量。由于 \(U\) 是一个实对称矩阵，所以一定存在 6 个线性无关的特征向量。
你当然可以直接硬算，但是手动求一个 6 阶矩阵的特征值还是一件挺麻烦的事情，鉴于搞数学的人一般比较懒，我们可以换个思路想一想。
注意到这个系统具有对称性，其对称群是 \(S_3\)。\(S_3\) 这个群是集合 \(\{1,2,3\}\) 的置换群，同时也是平面上正三角形的对称群，在后者的情形通常称为二面体群 \(D_3\)。
回忆 \(S_3\) 的一个表现为 \[S_3=\{a,b\mid a^2=b^3=(ab)^2=1\}.\] 当作为置换群时，\(a=(12),\,b=(123)\)。当作为二面体群时，\(a=\left(\begin{smallmatrix}-1&0\\0&1\end{smallmatrix}\right)\) 是关于 \(y\) 轴的反射，\(b=\left(\begin{smallmatrix}\cos2\pi/3&-\sin2\pi/3\\\sin2\pi/3&\cos2\pi/3\end{smallmatrix}\right)\) 是关于原点角度为 \(2\pi/3\) 的旋转。
系统状态 \(\mathbf{q}\) 所在的空间 \(\mathbb{R}^6\) 是三个 \(\mathbb{R}^2\) 的直和：\(\mathbb{R}^6=\mathbb{R}^2_A\oplus\mathbb{R}^2_B\oplus\mathbb{R}^2_C\)。其中 \(\mathbb{R}^2_A,\mathbb{R}^2_B,\mathbb{R}^2_C\) 分别是 \(A,B,C\) 的坐标空间。\(S_3\) 在置换这三个直和项的同时，又以 \(D_3\) 的方式作用在每个直和项上，所以这个表示是 \(S_3\) 的置换表示和在 \(\mathbb{R}^2\) 上二维表示的张量积。
例如，对换 \((12)\) 交换 \(A,B\)，同时将它们的坐标关于 \(y\) 轴作反射： \[\begin{aligned} A\otimes (q_1,q_2) &\xrightarrow{(12)} B\otimes(-q_1,q_2),\\ B\otimes (q_3,q_4) &\xrightarrow{(12)} A\otimes(-q_3,q_4). \end{aligned}\]
我们把这个张量积表示记作 \(\rho\)，并记 \[R=\begin{pmatrix}\cos\frac{2\pi}{3}&-\sin\frac{2\pi}{3}\\\sin\frac{2\pi}{3}&\cos\frac{\pi}{3}\end{pmatrix},\quad S=\begin{pmatrix}-1&0\\0&1\end{pmatrix}.\]
我们可以明确写出 \(a=(12)\) 在这个张量积表示下的矩阵：\(a\) 作为置换对应的矩阵是 \[A=\begin{pmatrix}0&1&0\\1&0&0\\0&0&1\end{pmatrix}.\] 在二面体群 \(D_3\) 中，\(a\) 是关于 \(y\) 轴的反射，其矩阵为 \(S\)，所以 \(a\) 在 \(\mathbb{R}^3\otimes\mathbb{R}^2\) 上的作用对应的矩阵是 Kronecker 乘积 \(A\otimes S\)。
下面列出了 \(S_3\) 的各个元素在 \(\rho\) 下对应的矩阵：
\[ \begin{align*} \rho(e)&=I_3\otimes I_2=\begin{pmatrix}I_2&0&0\\0&I_2&0\\0&0&I_2\end{pmatrix},\\ \rho(a)&=\begin{pmatrix}0&1&0\\1&0&0\\0&0&1\end{pmatrix}\otimes S=\begin{pmatrix}0&S&0\\S&0&0\\0&0&S\end{pmatrix},\\ \rho(b)&=\begin{pmatrix}0&1&0\\0&0&1\\1&0&0\end{pmatrix}\otimes R=\begin{pmatrix}0&R&0\\0&0&R\\R&0&0\end{pmatrix},\\ \rho(b^2)&=\begin{pmatrix}0&0&1\\1&0&0\\0&1&0\end{pmatrix}\otimes R^2=\begin{pmatrix}0&0&R^2\\R^2&0&0\\0&R^2&0\end{pmatrix},\\ \rho(ab)&=\begin{pmatrix}0&0&1\\0&1&0\\1&0&0\end{pmatrix}\otimes SR=\begin{pmatrix}0&0&SR\\0&SR&0\\SR&0&0\end{pmatrix},\\ \rho(ab^2)&=\begin{pmatrix}1&0&0\\0&0&1\\0&1&0\end{pmatrix}\otimes SR^2=\begin{pmatrix}SR^2&0&0\\0&0&SR^2\\0&SR^2&0\end{pmatrix}. \end{align*} \]
\(S_3\) 在表示 \(\rho(g)\) 下显然都是正交矩阵，而且保持系统的势能不变，所以对任何状态 \(\mathbf{q}\) 有 \[V(\rho(g)\mathbf{q})=V(\mathbf{q}),\] 即 \[{\bf q^T}\rho(g)^TU\rho(g){\bf q}=U.\] 由于 \(\rho(g)\) 正交所以 \(\rho(g)U=U\rho(g)\)，从而 \(U\) 是表示 \(\rho\) 的一个自同态。
在数学上，我们非常喜欢这种与一个表示 \(\rho\) 交换的矩阵，因为这种矩阵的任何特征子空间都是 \(\rho\) 的不变子空间，即给出 \(\rho\) 的子表示，从而可以帮助我们更好地理解 \(\rho\) 的结构。不过在这个问题中，我们要反过来借助 \(\rho\) 的分解来分析 \(U\) 的特征子空间的结构。
我们来确定表示 \(\rho\) 的结构。注意到 \(S_3\) 在 \(\{1,2,3\}\) 上的置换表示，其特征只有在单位元 \(e\) 处不为 0（值是 3），在任何非单位元 \(g\in S_3\) 处都是 0。这个表示是张量积表示 \(\rho\) 的分量，所以 \(\rho\) 的特征 \(\chi\) 也具有此性质。显然 \(\chi(e)=6\)，于是 \(\chi\) 与 \(S_3\) 的正则表示的特征完全相同，从而同构于正则表示，从而 \(\chi\) 可以分解为两个一次表示和两个二次不可约表示的和： \[\chi = \chi_1 + \chi_2 + \chi_3+\chi_4.\] 其中 \(\chi_1\) 是平凡表示的特征，\(\chi_2\) 是符号表示的特征（偶置换为 +1，奇置换为 -1），这两个特征都是一次的。\(\chi_3=\chi_4\) 是 \(S_3\) 作为二面体群的二维不可约表示的特征。
记 \(\chi_i\) 对应的不可约模是 \(V_i\)，则 \(\dim V_1=\dim V_2=1\)，\(\dim V_3=\dim V_4=2\) 并且 \[\mathbb{R}^6=V_1\oplus V_2\oplus V_3\oplus V_4.\]
\(\mathbb{R}^6\) 是 \(U\) 的特征子空间的直和，而 \(U\) 的特征子空间都是 \(\rho\) 的不变子空间，从而可以分解为 \(\rho\) 的不可约模的直和。这说明每个 \(V_i\) 都包含在 \(U\) 的某个特征值 \(\lambda_i\) 的特征子空间中。即 \(U\) 在 \(V_i\) 上的作用是数乘 \(\lambda_i\)。
从 \(V_1,\ldots,V_4\) 中分别选择一组基，它们合起来构成 \(\mathbb{R}^6\) 的一组基。在这组基下 \(U\) 是对角矩阵，形如 \[U=\begin{pmatrix}\lambda_1&0&0&0\\0&\lambda_2&0&0\\0&0&\lambda_3I_2&0\\0&0&0&\lambda_4I_2\end{pmatrix}.\] 同时 \(\rho(g)\) 形如 \[\rho(g)=\begin{pmatrix}D_1&0&0&0\\0&D_2&0&0\\0&0&D_3&0\\0&0&0&D_4\end{pmatrix}.\]
我们来计算 \(\rho(g)U\) 对不同 \(g\in S_3\) 的迹。首先注意到 \[\mathop{\mathrm{tr}}{\rho(g)U}=\mathop{\mathrm{tr}}{\begin{pmatrix}\lambda_1D_1&0&0&0\\0&\lambda_2D_2&0&0\\0&0&\lambda_3D_3&0\\0&0&0&\lambda_4D_4\end{pmatrix}}=\sum_{i=1}^4\lambda_i\chi_i(g). \]
另一方面，我们对 \(S_3\) 中的 \(e,a,b\) 这三个元素，根据前面列出的 \(\rho(g)\) 矩阵，计算其与 \(U\) 的乘积，再求迹得到（这是本文计算量最大的部分！） \[ \begin{align*} \mathop{\mathrm{tr}}{\rho(e)U}&=\mathop{\mathrm{tr}}{U}=\frac{1}{4}(5+3+5+3+2+6)=6,\\ \mathop{\mathrm{tr}}{\rho(a)U}&=\mathop{\mathrm{tr}}{\begin{pmatrix}0&S&0\\S&0&0\\0&0&S\end{pmatrix}\frac{1}{4}\begin{pmatrix}5&\sqrt{3}&-4&0&-1&-\sqrt{3}\\ \sqrt{3}&3&0&0&-\sqrt{3}&3\\ -4&0&5&-\sqrt{3}&-1&\sqrt{3}\\ 0&0&-\sqrt{3}&3&\sqrt{3}&-3\\ -1&-\sqrt{3}&-1&\sqrt{3}&2&0\\ -\sqrt{3}&-3&\sqrt{3}&-3&0&6 \end{pmatrix}}\\ &=\frac{1}{4}(4+0+4+0-2+6)=3,\\ \mathop{\mathrm{tr}}{\rho(b)U}&=\mathop{\mathrm{tr}}{\begin{pmatrix}0&R&0\\0&0&R\\R&0&0\end{pmatrix}\frac{1}{4}\begin{pmatrix}5&\sqrt{3}&-4&0&-1&-\sqrt{3}\\ \sqrt{3}&3&0&0&-\sqrt{3}&3\\ -4&0&5&-\sqrt{3}&-1&\sqrt{3}\\ 0&0&-\sqrt{3}&3&\sqrt{3}&-3\\ -1&-\sqrt{3}&-1&\sqrt{3}&2&0\\ -\sqrt{3}&-3&\sqrt{3}&-3&0&6 \end{pmatrix}}\\ &=\frac{1}{4}(2+0-1+3+2+0)=\frac{3}{2}. \end{align*} \] 于是我们得到三个方程 \[ \begin{align*} 6&=\lambda_1+\lambda_2+2(\lambda_3+\lambda_4),\\ 3&=\lambda_1-\lambda_2,\\ 3/2&=\lambda_1+\lambda_2-(\lambda_3+\lambda_4). \end{align*} \] 于是 \(\lambda_1=3\)，\(\lambda_2=0\)，\(\lambda_3+\lambda_4=3/2\)。
我们还缺一个方程！可以用 \(\mathop{\mathrm{tr}}{U^2}=\lambda_1^2+\lambda_2^2+2(\lambda_3^2+\lambda_4^2)\) 来做，但手算 \(U^2\) 的话计算量还是不小的。更简单的办法是用物理直观：我们已经看到平移和旋转是两种简正模式，这两种模式下质点的振动频率是 0，而平移包含了 \(x\) 轴和 \(y\) 轴两个线性无关的方向上的平移，所以 0 作为 \(U\) 的特征值至少是三重的。我们已经解得 \(\lambda_2=0\) 是一个，所以 \(\lambda_3\) 和 \(\lambda_4\) 中必然还有一个是 0，不妨设 \(\lambda_3=0\)，则 \(\lambda_4=3/2\)。
得到了 \(\lambda_1,\lambda_2,\lambda_3,\lambda_4\)，对应的频率就可以用 \(\omega_i=\sqrt{\frac{\lambda_ik}{m}}\) 算出来。
总结一下，系统总共有 4 种简正模式：
平凡表示 (\(\lambda_1=3\)) 对应的简正模式是呼吸，其频率为 \(\omega=\sqrt{\frac{3k}{m}}\)：
符号表示 (\(\lambda_2=0\)) 对应的简正模式是旋转，其频率 \(\omega=0\)：
第一个二维不可约表示 (\(\lambda_3=0\)) 包含了两种简正模式，它们分别是沿着 \(x\) 方向和 \(y\) 方向的平移，其频率 \(\omega=0\)。
第二个二维不可约表示 (\(\lambda_4=3/2\)) 也包含了两种简正模式，它们分别是两个不同方向上的“鼓掌”：
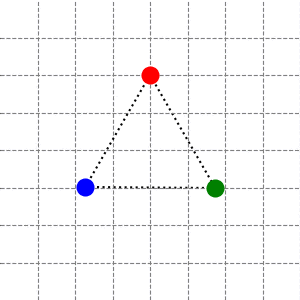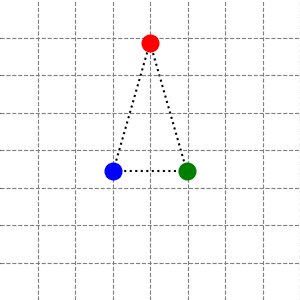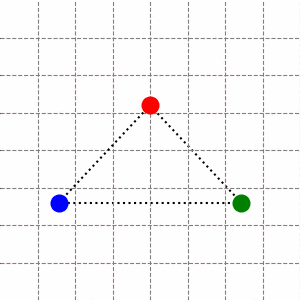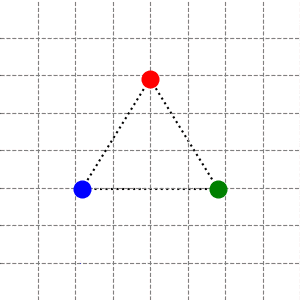
另一种可以由上面的旋转 \(2\pi/3\) 后得到。这两个简正模式的频率都是 \(\omega=\sqrt{\frac{3k}{2m}}\)。
至此我们就求出了系统的全部简正模式。