Coxeter 群笔记(四):有限、仿射、双曲三种情形的 Tits 锥
本文主要参考了 (Howlett, Rowley, and Taylor 1997)。
书接 上回,我们来研究当 \(W\) 分别是有限、仿射和双曲三种情形时,其 Tits 锥 \(\mathcal{C}\) 和对偶锥 \(\mathcal{C}^\ast\) 的结构。
我们约定 \((W,S)\) 总是一个有限生成、不可约的 Coxeter 系。
有限
关于 Coxeter 群的一个熟知的结论是,\(W\) 是有限群当且仅当内积 \((\cdot,\cdot)\) 是正定的 (见 Humphreys 1990, sec. 6.4)。我这里略过对此结论的证明(否则篇幅会拉的太长)。我们来证明这还等价于 \(\mathcal{C}=V^\ast\):
定理 1.1. Tits 锥 \(\mathcal{C}=V^\ast\) 当且仅当 \(W\) 是有限群。
例: 在下图中,\(W\) 是正二十面体群 \(H_3\),红色的锥是基本区域,它在 \(W\) 的作用下铺满了整个空间,所以 \(\mathcal{C}=\mathbb{R}^3\)。\(\mathcal{C}\) 与球面的交给出球面上的密铺。

证明:
\(\Rightarrow\): \(\mathcal{C}=V^\ast\) 当然可以推出 \(-\mathcal{D}\in\mathcal{C}\)(\(\mathcal{D}\) 是基本区域),而对任何 \(x\in-\mathcal{D}\) 都有 \(\Phi^+\subseteq \mathrm{Neg}(x)\),根据前文得到的 Tits 锥的刻画,\(|\Phi^+|=|\mathrm{Neg}(x)|<\infty\),从而 \(\Phi^+\) 是有限集,从而 \(\Phi\) 也是有限集。根据我们在根系一文中证明过的另一个 结论,\(W\) 是有限群。
\(\Leftarrow\): \(W\) 是有限群说明 \(\Phi\) 也是有限的,从而对任何 \(x\in V^\ast\) 都有 \(|\mathrm{Neg}(x)|\leq |\Phi^+|<\infty\),从而 \(x\in\mathcal{C}\)。\(\blacksquare\)
无限群的 Tits 锥
在仿射和双曲的情形,Coxeter 群都是无限群。我们来介绍一点关于无限 Coxeter 群 Tits 锥的一般结论。
命题 2.1. 设 \(W\) 是不可约 Coxeter 群。如果存在 \(J\subsetneqq S\) 使得 \(\Phi\setminus\Phi_J\) 是有限集,则 \(W\) 必然是有限群。
证明:由于 \(J\subsetneqq S\),所以可以设 \(S\setminus J=\{s_1,\ldots,s_r\}\,(r\geq1)\)。由于 \(W\) 不可约,\(W\) 的 Coxeter 图 \(\Gamma\) 是连通的,\(J\) 中的任何顶点都可以通过某条路径与 \(S\setminus J\) 中的顶点相连。记 \(d(s)\) 是顶点 \(s\) 与 \(S\setminus J\) 之间的最短距离,将 \(S\) 按如下方式重新排序为 \(S=\{s_1,\ldots,s_n\}\): \[S = \underbrace{\overbrace{\{s_1,\ldots,s_r\}}^{d(s)=0}}_{S\setminus J}\cup\underbrace{ \overbrace{\{s_{r+1},\ldots,s_{r+k}\}}^{d(s)=1},\overbrace{\{s_{r+k+1},\ldots\}}^{d(s)=2},\cdots}_{J}\,.\]
即 \(S\setminus J\) 中的顶点排在最前面,接下来是那些与 \(S\setminus J\) 距离为 1 的顶点,然后是与 \(S\setminus J\) 距离为 2 的顶点,等等。
\(\Phi^+\) 可以表示为 \(n\) 个不相交集合的并:记 \(\Phi_i^+\) 是所有可以由 \(\{\alpha_i,\ldots,\alpha_n\}\) 张成,且 \(\alpha_i\) 项系数不为 0 的正根组成的集合: \[\Phi_i^+=\{\lambda\mid \lambda\in\Phi^+,\ \lambda=\sum_{j=i}^nc_j\alpha_j,\ c_i\ne 0\}.\] 则不难看出有 \(\Phi^+=\Phi_1^+\sqcup\cdots\sqcup\Phi^+_n\),以及 \(\Phi^+\setminus\Phi_J^+=\Phi_1^+\cup\cdots\cup\Phi^+_r\)。由于假设了 \(\Phi\setminus\Phi_J\) 是有限的,所以 \(\Phi_1^+,\ldots,\Phi^+_r\) 都是有限的。
我们用归纳法依次论证 \(\Phi^+_{r+1},\ldots,\Phi^+_{n}\) 也都是有限集:设 \(r+1\leq i\leq n\) 且已知对所有 \(j<i\),\(\Phi_1^+,\ldots,\Phi^+_j\) 都是有限集, 现在考察 \(\Phi^+_i\),注意必然有 \(d(s_i)\geq1\),所以存在 \(j<i\) 使得 \(d(s_j)<d(s_i)\) 且 \(s_j\sim s_i\)。
我们发现:
- \(s_j\Phi_i^+\) 的元素都是正根。这是因为用 \(s_j\) 作用不改变 \(\Phi^+_i\) 中元素的 \(\alpha_i\) 项系数;
- \(s_j\Phi_i^+\subset\Phi^+_j\)。这是因为若 \(\lambda=\sum_{k\geq i}c_k\alpha_k\in\Phi^+_i\),则 \[s_j\lambda=\lambda-2\left(\sum_{k\geq i}c_k(\alpha_k,\alpha_j)\right)\alpha_j.\] 上面每一项 \(c_k(\alpha_k,\alpha_j)\) 都非正,且由于顶点 \(s_i,s_j\) 相邻所以 \(c_i(\alpha_i,\alpha_j)<0\)。所以 \(s_j\lambda\) 的 \(\alpha_j\) 项系数严格大于 0。
于是 \(|\Phi_i^+|\leq |\Phi^+_j|\) 也是有限集。从而所有 \(\Phi^+_1,\ldots,\Phi^+_n\) 都是有限集,从而 \(\Phi\) 也是有限的。由于 \(W\) 和 \(\Phi\) 同为有限或者无限,所以 \(W\) 是有限群,命题得证。\(\blacksquare\)
命题 2.1 有如下的推论:
推论 2.2. 如果 \(W\) 不可约且是无限群,则 Tits 锥 \(\mathcal{C}\) 满足 \(\mathcal{C}\cap-\mathcal{C}=\{0\}\),从而 \(\mathcal{C}\) 是一个点锥 (pointed cone)。
证明:由于 \[\mathcal{C}\cap-\mathcal{C}=\bigcup_{w_1,w_2\in W}w_1\overline{\mathcal{D}}\cap w_2(-\overline{\mathcal{D}}),\] 所以若 \(\mathcal{C}\cap-\mathcal{C}\ne\{0\}\) 则存在 \(x\ne0\in\overline{\mathcal{D}}\) 和 \(w\in W\) 满足 \(-wx\in\overline{\mathcal{D}}\)。令 \[J=\{s\in S\mid \langle \alpha_s,\,x\rangle=0\}\] 是经过 \(x\) 的那些镜子。\(x\ne 0\) 说明 \(J\subsetneqq S\) 是真子集。
对任何 \(\lambda\in\Phi^+\setminus\Phi^+_J\),显然 \(\langle \lambda,\,x\rangle>0\),并且对这样的 \(\lambda\) 有 \[\langle w\lambda,\,-wx\rangle = \langle \lambda,\,-x\rangle<0.\] 而 \(-wx\in\overline{\mathcal{D}}\),所以 \(w\lambda\) 是负根,从而 \(\Phi^+\setminus\Phi^+_J\subset\mathrm{Neg}(w)\),从而 \[|\Phi^+\setminus\Phi^+_J|\leq |\mathrm{Neg}(w)|=l(w)<\infty.\] 由 命题 2.1 \(W\) 是有限群,这与已知矛盾。\(\blacksquare\)
推论 2.3. 如果 \(W\) 不可约且是无限群,则对偶锥 \(\mathcal{C}^\ast\ne\{0\}\)。
证明:用反证法,若不然,则 \(\overline{\mathcal{C}}=\mathcal{C}^{\ast\ast}=V^\ast\) 是全空间。由于一个凸集的内点和它的闭包的内点集相同(证明见这个 附件),所以 \(\mathcal{C}=V\),这与 推论 2.2 的结论 \(\mathcal{C}\) 是点锥矛盾。\(\blacksquare\)
仿射
在本节中,我们需要如下关于不可约仿射 Coxeter 群的事实 (见 Humphreys 1990, secs. 2.6, 6.5)。
设 \(W\) 是不可约、仿射 Coxeter 群,则:
- \(\mathrm{rad}(V)\) 的维数是 1,它由一个向量 \(\delta=\sum_{s\in S}z_s\alpha_s\) 生成,其中每个 \(z_s>0\)。
- \(\delta\) 的坐标 \(z=(z_1,\ldots,z_s)^T\) 满足 \(Az=z^TAz=0\),其中 \(A=((\alpha_s, \alpha_t))_{s,t\in S}\) 是内积 \((\cdot,\cdot)\) 的 Gram 矩阵。
- \(w\delta=\delta\) 对所有 \(w\in W\) 成立。
- \(A\) 的任何 \(\leq n-1\) 阶主子式都是正定的。
我们花点笔墨解释一下这几个事实的含义。回忆 \(W\) 称作仿射是指内积 \((\cdot,\cdot)\) 是半正定但不是正定的。这个定义中没有要求 \((\cdot,\cdot)\) 的符号中有几个 0,但是上面的结论 1, 2 告诉我们,在 \(W\) 不可约的前提下,\((\cdot,\cdot)\) 的符号中有且只有一个 0,并且 \(\mathrm{rad}(V)\) 由一个向量 \(\delta\) 生成。\(\delta\) 的所有系数都非零并且同号,并且 \(W\) 保持 \(\delta\) 不动。
我们可以利用 1, 2 来快速验证一下 3。由 \(z^TA=0\) 可得对任何 \(t\in S\) 有 \[\sum z_s(\alpha_s,\alpha_t)=(\delta,\alpha_t)=0.\] 从而 \(t(\delta)=\delta-2(\delta,\alpha_t)\alpha_t=\delta\),即任何单反射保持 \(\delta\) 不动,从而 \(W\) 保持 \(\delta\) 不动。
4 说的是对任何 \(I\subsetneqq S\),标准椭圆子群 \(W_I\) 都是有限群;或者等价地,从 \(W\) 的 Coxeter 图 \(\Gamma\) 中删去至少一个顶点以后,剩下的子图是有限的。
定理 3.1. 在仿射的情形 \(\mathcal{C}^\ast\) 是一条射线:\(\mathcal{C}^\ast=\{c\delta\mid c\geq0\}\),Tits 锥是以 \(\delta\) 为法向量的半空间加上原点:\(\mathcal{C}=\{0\}\cup\{\delta > 0\}\)。
例: 在下图中,\(W\) 是仿射 \(\widetilde{A}_2\),红色的锥是基本区域,它在 \(W\) 的作用下铺满了整个上半空间,所以 \(\mathcal{C}=\{z>0\}\cup\{0\}\)。\(\mathcal{C}\) 与平面 \(z=1\) 的交给出二维的 Euclidean 密铺。
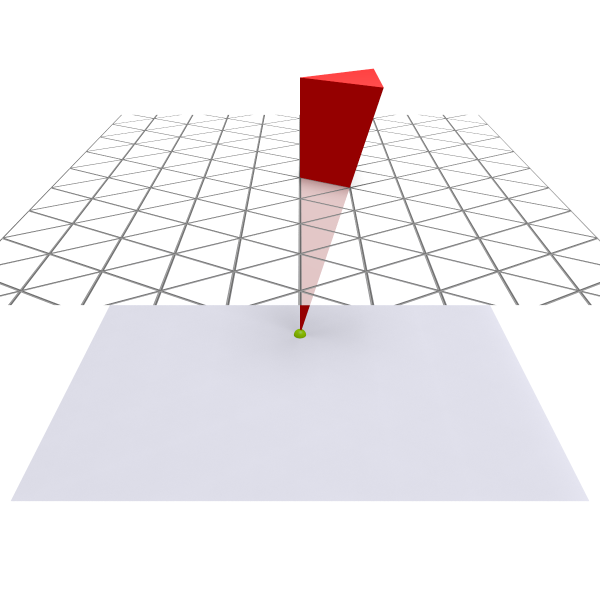
证明:我们已经知道 \(\mathrm{rad}(V)=\mathbb{R}\delta\)。根据 推论 2.3,\(\mathcal{C}^\ast\) 包含某个非零向量 \(v\)。由 \((v,v)\leq0\) 以及 \((\cdot,\cdot)\) 半正定,所以 \((v,v)=0\),即 \(v\in\mathrm{rad}(V)\)。从而 \(\{0\}\ne\mathcal{C}^\ast\subseteq\mathbb{R}\delta\)。再结合 \(\mathcal{C}^\ast\) 是点锥,所以 \(\mathcal{C}^\ast\) 只能是 \(\mathbb{R}_{\geq0}\delta\) 或者 \(\mathbb{R}_{\leq0}\delta\)。但由于 \(\delta\) 是 \(\Delta\) 的正线性组合,\(-\delta\notin\mathrm{cone}(\Delta)\),所以 \(\mathcal{C}^\ast=\mathbb{R}_{\geq0}\delta\)。这就给出了对偶锥 \(\mathcal{C}^\ast\) 的刻画。
再来分析 Tits 锥 \(\mathcal{C}\)。取对偶得到 \(\overline{\mathcal{C}}=\mathcal{C}^{\ast\ast}=\{\delta\geq0\}\)。由于一个凸集的内点和它的闭包的内点集相同,所以 \(\mathcal{C}^\circ=\{\delta>0\}\),于是 \[\{\delta>0\}\subset\mathcal{C}\subset\overline{ \mathcal{C} }=\{\delta\geq0\}.\]
对任何 \(x\in\{\delta=0\}\),若 \(x\in\mathcal{C}\),则存在 \(w\in W\) 和 \(y\in\overline{\mathcal{D}}\) 使得 \(x=wy\)。于是 \[0 = \langle \delta,\,x\rangle=\langle \delta,\,wy\rangle=\langle w^{-1}\delta,\,y\rangle=\langle \delta,\,y\rangle=\sum_{s\in S}z_s\langle \alpha_s,\,y\rangle.\] 然而每个 \(z_s>0\),并且由于 \(y\in\overline{\mathcal{D}}\) 所以每个 \(\langle \alpha_s,\,y\rangle\geq0\),这只能是 \(\langle \alpha_s,\,y\rangle=0\) 对所有 \(\alpha_s\in\Delta\) 成立。结合 \(\Delta\) 是 \(V\) 的一组基,这导致 \(y=0\),从而 \(x=0\),所以超平面 \(\{\delta=0\}\) 中属于 \(\mathcal{C}\) 的只有 0。这就证明了 \(\mathcal{C}=\{0\}\cup\{\delta>0\}\)。\(\blacksquare\)
双曲
双曲的情形 Tits 锥的结构要复杂许多,一般来说没有完整的刻画。
我们首先来介绍一些关于 Lorentzian 内积的基本知识。这些内容在 (Ratcliffe 2006, vol. 149, chap. 3) 中都可以找到。
设 \(V\) 是一个 \(n\) 维实向量空间,其上有一个内积 \((\cdot,\cdot)\)。我们用 \((p,q)\) 表示 \((\cdot,\cdot)\) 的正负惯性指数。当 \((p,q)=(n-1,1)\) 时,\(V\) 是一个 Lorentzian 空间。我们称 \(v\in V\) 是
- space-like 的,如果 \((v,v)>0\);
- light-like 的,如果 \((v,v)=0\);
- time-like 的,如果 \((v,v)<0\)。
注: space-like, light-like, time-like 这三个术语我不作翻译,保持英文原样似乎更容易理解?
这个定义也可以推广到 \(V\) 的子空间中:如果 \(U\subset V\) 是一个子空间,我们称 \(U\) 是
- space-like 的,如果 \((\cdot,\cdot)\mid_U\) 是正定的;
- light-like 的,如果 \((\cdot,\cdot)\mid_U\) 是半正定的,但不是正定的;
- time-like 的,如果 \(U\) 包含 time-like 的向量。
由于 Lorentzian 内积是非退化的,所以对任何子空间 \(U\) 都有 \(\dim U + \dim U^\bot=n\) 成立。
下面的命题是关于二次型知识的简单练习,我省略它们的证明。
命题 4.1.
- \(U\) 是 space-like 的当且仅当 \(U^\bot\) 是 time-like 的;
- \(U\) 是 light-like 的当且仅当 \(U^\bot\) 是 light-like 的。
取 \(z\) 是满足 \((z,z)=-1\) 的 time-like 的向量,记 \(U=\mathbb{R}z\),则 \(U^\bot\) 是 space-like 的并且有 \(V=U\oplus U^\bot\) 成立。于是任何 \(v\in V\) 可以写成 \(v = x + cz\) 的形式,这里 \(x\in U^\bot\) 是一个 Euclidean 空间中的向量,\(c\in\mathbb{R}\)。记 \[\mathcal{Q}=\{v\in V\mid (v,v)\leq 0\}\] 是所有非 space-like 的向量组成的集合,则 \(v=x+cz\in\mathcal{Q}\) 当且仅当 \((x,x)-c^2\leq0\)。
\(\mathcal{Q}\) 由上、下两个分支 \(\mathcal{Q}_+,\,\mathcal{Q}_-\) 组成,它们分别由 \(\mathcal{Q}\) 中满足 \(c\geq0\) 和 \(c\leq0\) 的点组成。\(\mathcal{Q}_+=-\mathcal{Q}_-\) 并且 \(\mathcal{Q}_+\cap\mathcal{Q}_-=\{0\}\)。
设 \(u,v\) 是两个非零向量,我们用记号 \(u\sim v\) 表示 \(u,v\) 属于同一个分支,即 \(u,v\) 同时属于 \(\mathcal{Q}_+\) 或者同时属于 \(\mathcal{Q}_-\);用记号 \(u\not\sim v\) 表示 \(u,v\) 属于不同的分支,即 \(u,v\) 一个属于 \(\mathcal{Q}_+\),另一个属于 \(\mathcal{Q}_-\)。
命题 4.2 ((Ratcliffe 2006, thm. 3.1.1)). 设 \(u,v\in \mathcal{Q}-\{0\}\)。
- 如果 \(u\sim v\) 则 \((u,v)\leq0\)。
- \((u,v)=0\) 当且仅当 \(u,v\) 是共线的 light-like 的向量。
命题 4.2 的显然推论是:
推论 4.3. 设 \(u,v\in\mathcal{Q}-\{0\}\)。
- 若 \((u,v)>0\) 则 \(u\not\sim v\)。
- 若 \((u,v)\leq0\),且 \(u,v\) 中至少有一个是 time-like 的,则 \(u\sim v\)。
记 \(\mathcal{Q}_+\) 和 \(\mathcal{Q}_-\) 的内点分别为 \(\mathcal{N}_+\) 和 \(\mathcal{N}_-\),\(\mathcal{N}_+\) 和 \(\mathcal{N}_-\) 分别是 \(\mathcal{N}=\{v\in V\mid (v,v)<0\}\) 的两个连通分支。
由于 Lorentzinian 内积是非退化的,所以我们可以把 \(V\) 和 \(V^\ast\) 等同起来,这样 \(\mathcal{C}\) 和 \(\mathcal{C}^\ast\) 都在 \(V\) 中。我们将证明这时 Tits 锥的闭包 \(\overline{ \mathcal{C} }\) 必然包含 \(\mathcal{Q}_+,\,\mathcal{Q}_-\) 中的一个,同时与另一个的交只有 \(\{0\}\)。
首先由 前文中证明的结论,\(\mathcal{C}^\ast\) 中的向量相互之间的内积非正,特别地对任何 \(v\in\mathcal{C}^\ast\) 有 \((v,v)\leq0\),所以 \(\mathcal{C}^\ast\subset\mathcal{Q}\)。
命题 4.4. 在 \(W\) 不可约且双曲的情形,\(\mathcal{C}^\ast\cap \mathcal{Q}_+,\,\mathcal{C}^\ast\cap\mathcal{Q}_-\) 中必有一个是 \(\{0\}\)。
证明:若不然,设 \(u\in\mathcal{C}^\ast\cap\mathcal{Q}_+,\,u'\in \mathcal{C}^\ast\cap\mathcal{Q}_-\) 是非零向量,\(u=x+cz,\,u'=y+dz\) 是 如前所述的分解,则 \(c>0,\,d<0\)。考察 \[v=cu'-du=cy-dx\in(\mathbb{R}z)^\bot.\] \(v\) 是 \(u\) 和 \(u'\) 的非负线性组合,所以 \(v\) 也属于 \(\mathcal{C}^\ast\),从而 \((v,v)\leq0\)。结合 \((\mathbb{R}z)^\bot\) 是 space-like 的可得 \(v=0\),于是 \(cu'=du\)。由于 \(c,d\) 异号所以 \(u\) 和 \(-u\) 同时属于 \(\mathcal{C}^\ast\),但 \(\mathcal{C}^\ast\) 是点锥,所以 \(u=0\)。从而 \(\mathcal{C}^\ast\cap\mathcal{Q}_+\) 和 \(\mathcal{C}^\ast\cap\mathcal{Q}_-\) 中必有一个等于 \(\{0\}\)。\(\blacksquare\)
推论 4.5. 在双曲的情形,必有 \(\mathcal{C}^\ast\subset\mathcal{Q}_+\) 或者 \(\mathcal{C}^\ast\subset\mathcal{Q}_-\) 之一成立。
证明:结合 命题 4.4 和 \(\mathcal{C}^\ast\subset\mathcal{Q}=\mathcal{Q}_+\cup\mathcal{Q}_-\) 即得。\(\blacksquare\)
推论 4.6. 在双曲的情形,如果 \(\mathcal{C}^\ast\subset\mathcal{Q}_+\) 则 \(\mathcal{C}\supset \mathcal{N}_-\)。反之若 \(\mathcal{C}^\ast\subset\mathcal{Q}_-\) 则 \(\mathcal{C}\supset\mathcal{N}_+\)。
证明:首先注意到对任何 \(x\in\mathcal{Q}_+\) 和 \(y\in\mathcal{Q}_-\) 有 \((x,y)\geq0\),所以 \(\mathcal{Q}_+\) 和 \(\mathcal{Q}_-\) 互相包含在对方的对偶锥中。
由 推论 4.5,不妨设 \(\mathcal{C}^\ast\subseteq\mathcal{Q}_+\),取对偶以后有 \(\overline{\mathcal{C}}=\mathcal{C}^{\ast\ast}\supseteq \mathcal{Q}_+^\ast\supseteq\mathcal{Q}_-\),即 \(\overline{\mathcal{C}}\supset\mathcal{Q}_-\)。由于凸集的内点等于其闭包的内点,所以 \[\mathcal{C}^\circ=(\overline{ \mathcal{C} })^\circ\supset\mathcal{Q}_-^\circ=\mathcal{N}_-.\] \(\blacksquare\)
例: 以双曲群 \((7,3)\) 为例,红色的锥是 \(\overline{\mathcal{D}}\),Tits 锥 \(\mathcal{C}=\mathcal{N}_+\)。取 \(\mathcal{C}\) 与 hyperboloid 的交给出双曲密铺。
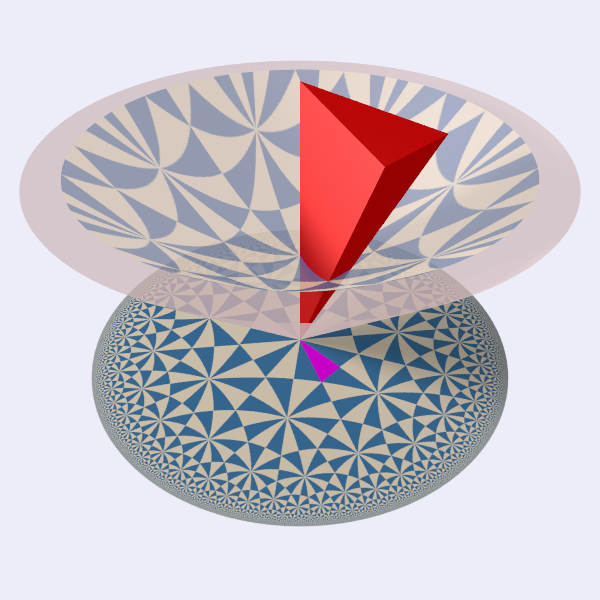
注意这里光锥是理想边界,光锥上的点(除 \(0\) 以外)无法经过有限次反射变换到基本区域中,所以理想边界不属于 \(\mathcal{C}\)。即 \(\mathcal{C}\subsetneqq \mathcal{Q}_+\)。
总结
下面的表格总结了有限、仿射、双曲三种情形 \(\mathcal{C}\) 和 \(\mathcal{C}^\ast\) 的结论:
| \(\phantom{}\) | \(\mathcal{C}\) | \(\mathcal{C}^\ast\) |
| 有限 | \(V^\ast\) | \(\{0\}\) |
| 仿射 | \(\{\delta>0\}\cup\{0\}\) | \(\mathbb{R}_{\geq0}\delta\) |
| 双曲 | 点锥且包含 \(\mathcal{N}_+,\mathcal{N}_-\) 之一 | 属于 \(\mathcal{Q}_+,\mathcal{Q}_-\) 之一 |
